レイトレーシング(14): 光沢面にトライ
これまでは物体表面での反射として完全拡散反射と完全鏡面反射のみ扱ってきた。ただ現実世界はほとんどが光沢のある表面(光沢面とする)なので、リアルな画像を生成するには光沢面のサポートが必須である。とくにぼやけたハイライトは3DCGの醍醐味(?)である。今回はそれを実装してみる。
0. Progressive Photon Mapping法に特化
その前に・・・
前回記事では、従来のPhoton Mapping法を用いたレイトレーシングプログラムに対し「オプションとして」Progressive Photon Mapping法(以下PPM法)による画質向上の機能を追加した。しかし作ってみると、このPPM法はこれまでのプログラムに比べ、かなり容易に表現力の向上が可能になるとわかった。たとえば「ちゃんとしたアンチエリアシング」や今回取り組む光沢面などである。
逆に、PPMでないと光沢面などの効果をシンプルに実装できないことから、今後はPPMを主体とすることにした。これにより、PPMを使うかどうかといったフラグや場合わけは排除し、PPMに特化した実装に変更する。結果として、実装はシンプルながらPPMの繰り返し回数を増やすほど高品質な画像が生成できるようになると期待する。
1. 光沢面の考え方
光沢面は完全拡散面と完全鏡面の中間となる表面状態である。

光子が物体表面に当たった時に、完全にランダム(拡散反射)でも完全に一方向(鏡面反射)でもなく、ある程度の確率で鏡面反射方向の周囲に分残して反射する。どの程度の確率でどれほど分散するかは表面の粗さ($roughness$)で表す。これが0なら完全に平滑で鏡面反射、1ならどの方向(交点から半球上のランダムな方向)へも反射しうるとする(ただ後述の通り、完全な拡散反射は諦めた)。
ここで「ハイライト」について言及しておきたい。昔からあるベタな3DCG画像では、床平面上に球体が置かれ、例えば球の右上ぐらいに明るいハイライトがぼんやりとした白い円で表現されている。このハイライトが画像のリアルさをぐっと引き上げる。昔ながらの手法ではこのハイライトを視線、光源方向などから計算で擬似的に求めていたわけだ。しかし実際のハイライトは「光源の映り込み」である。周りの物体が反射して映り込むのとなんら変わらない。ゆえにこれまでの記事の作例では球の上部に四角いエリアライトがそのまま映り込んでいる(完全鏡面反射だから)。

ではぼんやりしたハイライトはどうやってできるのかというと、物体表面がざらついているために、表面の微小なところでは、ある部分は光源が映り込み、ある部分は映り込まないといったことが起こっていて、それらを総合すると光源がぼんやり映ることになるからだ。
であれば、擬似的に計算でハイライトを「作る」のではなく、光源の映り込みという単純な処理でハイライトを表現できるようにしたい。PPMを使えばそれがうまくできそうだ。
2. 微小平面の法線
光沢面をサポートするために、光子/視線が反射する方向を$roughness$に応じてランダムに生成してやる必要がある。その方法には大きく下の2種類がある(と思う)。
- 交点から鏡面反射方向のベクトルを中心としてその周囲に広がった方向を生成する
- 交点の微小平面法線をランダムに生成し、それを基に反射方向を算出する
今回は2で実装することにした。理由は以下のとおり。
- 1の場合ランダムに方向を生成すると、入射方向寄りの方向が生成できない(わけではないが面倒に思った)(図2.2-a)
- 微小平面法線を使えば、反射ベクトルだけでなく屈折ベクトルも作り出せる(図2.2-b)
- マイクロファセット理論との相性がいいのではないか(と勝手に推測)

では実際の作り方だ。
- まず交点の法線ベクトル $n$ と光子/視線の入射ベクトル $e$ から、 $n$ と直行する交点平面上のベクトル $u$ , $v$ を外積を使って求める。(図2.3)

- 次にランダムな方向ベクトルを作るため、2つの一様乱数 $\xi_1 [0,1]$, $\xi_2 [0,1]$ を生成して下式を用いて上記直行ベクトルの長さを計算する($x$ , $y$ , $z$ とする)。 (参考: Realistic Image Synthesis - BRDFs and Direct Lighting - のp.5)
$ \displaystyle \qquad x = \cos{(2\pi\xi_1})\sqrt{(1-\xi_2^{\frac{2}{m+1}})} \ \qquad y = \xi_2^{\frac{1}{m+1}} \ \qquad z = \sin{(2\pi\xi_1})\sqrt{(1-\xi_2^{\frac{2}{m+1}})} $ 3. 直行ベクトルと各係数から微小平面の法線ベクトル $n'$ を求める。
これで法線ベクトル $n'$ を生成できた。ところで粗さ $roughness$ はどこへ行ったのだろうか?$roughness$ に応じてランダムに生成される$n'$ の拡がり具合が変わるようにするのではなかったか?上記の長さを計算する式に出てくる $m$ に注目してほしい。この $m$ を$0$ から $\infty$ まで変化させることにより生成される方向の拡がり具合を調整できる。$m$ が $0$ なら一様に拡散(完全拡散面)、$\infty$ なら $y$ 成分は常に $1$ (完全鏡面)となるので、$roughness [0,1]$ から $m$ を作り出せればよい。
$ \displaystyle \qquad roughness = 0 \rightarrow m = \infty $ $ \displaystyle \qquad roughness = 1 \rightarrow m = 0 $
さて問題は、上記のような変換ができ、かつ$roughness$の変化にできるだけリニア=見た目になだらかな変化、となるような関数をどう選ぶかである。いろいろ試行錯誤した結果、今回は下の式で生成することにした。
$ \displaystyle \qquad m = {({10}^6)}^{(1-\sqrt{roughness})} $
この式の意図は次の通り。
- $roughness$の変化に対し $ m $ の変化が逆(増えると減る)なので、揃えるために$1-roughness$ のような形にしたが、微調整のため $\sqrt{roughness}$ を使った。
- ${10}^6$としたのは「見た目になだらかな変化」となるような冪指数を試した結果。好み。
- $\infty$ は無理だが、$1-\sqrt{roughness}$が$1$なら非常に大きな数字になってほしいので指数関数を使った。
ただしこの式ではどんな$roughness [0,1]$ でも $m=0$にはできないので、完全拡散反射は表現できないが。
これで微小平面法線($n'$)を求めることができる。あとは交点法線 $n$ の代わりに$n'$ を使って光線追跡するだけで良い。なお、このようにランダムに法線を選んでしまうとその方向からくる光しかレンダリングに使えない(もっとあらゆる方向からくる光を集める必要があるのに)と思うが、そこでPPMが威力を発揮するわけだ。イテレーション回数を1000とすれば、ランダムに1000種類の方向をトレースした結果を総合できる。パストレーシングのように交点でランダムな多数のレイを生成して追跡、さらに先の交点でランダムな多数のレイを生成して・・・とすると追跡するレイが指数関数的に爆発するが、PPMではイテレーション回数で抑えられるので処理負荷を低くできる(ハズ)。最初のレイ、交点での反射方向のレイを確率で一つ選んで生成しているので、たぶん統計学的にもよい結果が得られる、と期待しよう。
3. 実装と作例
まず物体の材質を表すパラメータに$roughness$から生成される$ m $(を含めた冪指数)をpowerGlossyとして追加する。レンダリングのたびにこの計算を行うのを避けるためである。この冪指数を計算している関数がdensityPowerである。
densityPower :: Double -> Double
densityPower rough = 1.0 / (10.0 ** pw + 1.0)
where
pw = 6.0 * (1.0 - sqrt rough)
次に、ランダムな方向ベクトルを生成するdistributedNormalである。2つの乱数xi1, xi2を生成したあと、上記式に基づき係数x,y,zを求め、最後にまとめて法線ベクトルnvec'にしている。
distributedNormal :: Direction3 -> Double -> IO Direction3
distributedNormal nvec pow = do
xi1 <- MT.randomIO :: IO Double -- horizontal
xi2 <- MT.randomIO :: IO Double -- virtical
let
phi = 2.0 * pi * xi2
uvec0 = normalize $ nvec <*> (Vector3 0.00424 1.0 0.00764)
uvec = case uvec0 of
Just v -> v
Nothing -> fromJust $ normalize $ nvec <*> (Vector3 1.0 0.00424 0.00764)
vvec = uvec <*> nvec
xi1' = xi1 ** pow
rt = sqrt (1.0 - xi1' * xi1')
x = cos(phi) * rt
y = xi1'
z = sin(phi) * rt
nvec' = x *> uvec + y *> nvec + z *> vvec -- n'の生成
case normalize nvec' of
Just v -> return v
Nothing -> return ex3
あとはこれまで単純に交点法線を使っていたところを置き換えてやれば良い。
traceRay :: Screen -> Bool -> V.Vector Object -> V.Vector Light -> Int
-> PhotonMap -> Double -> Material -> Ray -> IO Radiance
traceRay !scr !uc !objs !lgts !l !pmap !radius !m0 !r@(_, vvec)
| l >= max_trace = return radiance0
| otherwise = do
case (calcIntersection r objs) of
Nothing -> return radiance0
Just (t, p, n, m, io) -> do -- n: 交点の法線ベクトル
: (中略)
nvec' <- if rough sf == 0.0
then return n
else distributedNormal n (powerGlossy sf)
let
(rdir, cos1) = specularReflection nvec' vvec --n'を使って反射ベクトルを求める
: (後略)
光沢面の作例を次に示す(図3.1-a,b,c)。それぞれ黄色いプラスチック、金、黄色みのガラスである。各球は左上から$roughness$ が0.0, 0.1, 0.2, 0.3, 0.4、下段が左から0.5, 0.6, 0.7, 0.8,1.0としてある。徐々にハイライトがぼやけているのがわかるだろう。またガラスでは球を透過して集光模様ができているが、これも$roughness$に応じてぼやけている。(イテレーション回数=300)



他の作例も示そう。


4. まとめ
今回は光沢面を扱えるよう機能拡張した。作例からもわかるようにぼんやりしたハイライトがそれなりの品質で表現できるようになったと思う。特に金属ではとても本物らしくみえる。
一方、この手のハイライトは鏡面反射BRDFとして研究されており、Cook-Torranceモデルがしばしば使われているそうだ(下式)。(物理ベースレンダリングを柔らかく説明してみる(4))
$ \displaystyle f_{r,s} = \frac{DGF}{4\langle n,l\rangle\langle n,v\rangle} $
式中の$D$ は微小面法線分布関数NDFといい、今回追加したランダムな反射方向ベクトルの生成と非常に深い関係がありそう・・・だが詳しく調べていない。また、$G$ で表される幾何減衰項も微小平面の凹凸による光の遮蔽を表現しているそうで、よりリアルな画像生成には不可欠と思われるがこれも今後の勉強ネタである。今後研究の上、プログラムに組み入れよう。
レイトレーシング(13): Progressive Photon Mapping (ただし本家ではない)
・・・なんと前回の記事から2年が経っている。何もしていないわけではないが記事にま とめる気力がなかったのだ。少しまとまった時間ができたので久しぶりに書こうと思う。
今回のソースはこちら。
1. 素のフォトンマッピングの課題
フォトンマッピング法による画像生成は従来の手法(パストレーシングなど)に比べかな り少ないレイ数でも間接光や集光模様を綺麗に表現できるとても素晴らしい手法だと思う。 とはいえフォトンマッピング法も完璧ではない。ある点の色(輝度)を求めるため、有限 のフォトンと有限の領域(面積)から放射輝度推定を行っているからである。完璧な画像 を得るためには、無限個のフォトン、無限小の領域で推定すればいいのだが、現実的には 不可能である。そのため、次のような課題がある(と思う)。
- フォトンデータをメモリに読み込む必要があり大量のフォトンを使った計算をするには 大量のメモリを持つコンピュータが必要。
- 放射輝度推定に必要なフォトンを抽出するためkd木というデータ構造を使っていて比較 的効率は良いようだが、フォトン数が増えると抽出にとても時間が掛かる。
- フォトン数を少なくすればノイズ(色の滲み)が多くなる。これは推定に使うフォトン が少ないので推定値と真の輝度との差が大きくなるため。
- ノイズを減らそうと思うと、より広い領域から多数のフォトンを集めれば良いが、余計 なフォトンも推定に使われ、また輝度値が周りと平均化され全体的にぼやけた画像にな る(影の縁が鋭くならない)。
このような課題に対応する手法はいろいろ提案されており、直系(?)の研究ではプログ レッシブフォトンマッピング法がある。これはさらに改良されてStocastic Progressive Photon Maapingとなっているそうだ。以下は参考URL。
ほかにも、いろいろ研究されているようだ。今回はこの中から Probabilistic Approach という手法を選択した。理由は次の通り。
- 放射輝度推定に使う領域サイズ(参照半径というらしい)を小さくしながら通常のフォ トンマッピングを実行するだけ=フォトンマッピング処理をこのアルゴリズム用に修正 する必要がない。
- 参照半径は繰り返し(イテレーション)毎に変えるが、i番目の繰り返しでの半径は数 式で求められるため、前後のイテレーションとは独立して実行できる。そのため複数の コンピュータによる並列処理も容易。
- 1回のイテレーションは少ないフォトン数で実行するためメモリが少なくて済む(これ はProgressive PM全般の特徴)
- 100回、1000回と多数のイテレーションを行うことで副次的な効果が簡単に実装できる。 例えばアンチエリアシング、被写界深度、グロス面などだ。
以後、この手法(Progressive Photon Mapping: Probabilistic Approach)をPPM-PAと書く ことにする。
2. PPM-PAの実装
-1. 輝度値出力と統合処理
上記の通り、このPPM-PAは従来のフォトンマッピングプログラムを(ほぼ)変更しなくて 済むのがウリの一つだ。参照半径を変化させて生成した画像を最後に平均すれば良い。ア ルゴリズムは論文にも書いてあるが、簡単な擬似コードで書くと以下の通り。
r_1 ← 初期の半径
for i = 0 to N { # Nはイテレーション回数
参照半径r_iでフォトンマッピング法を実行し画像データを保管
i+1番目の参照半径(r_i+1)を求める
}
全画像データの各画素値の平均を計算し保管
今回はちょっとサボってこの統合処理はRubyで記述した(util/iterator.rb)。詳細はコー ドを見て貰えばわかると思う。ところで従来はPPM形式の画像ファイルを出力する。つま り各画素はRGB 256階調の整数値だ。そのため一定以上の輝度値以上は255にクリッピング されている。PPM-PAでは輝度値を集計して平均する必要がある。でないと何百回、何千回 繰り返すと、ほとんどの画素は黒、所々に色が出るといった画像になるので、データを平 均すると値が小さくなりすぎて真っ黒な画像が出来上がるのだ。最初そこに気づかず単純 にPPMデータを足したため、ほぼ真っ黒の画像となってしまった。。。
ということで、フォトンマッピングプログラムには2点の小改造を実施した。
"progressive"フラグを追加する。
- 従来通りPPMの画像を出力したい場合と、PPM-PAのために一旦画像生成結果の輝度 値を書き出す場合を分けるため、"progressive"フラグをスクリーン設定ファイル に追加。値は"yes"か"no"である。
progressiveフラグに応じて出力をPPMか輝度値で出力する。
if (progressive scr) == True
then -- 輝度値を出力
forM_ [0..(V.length image - 1)] $ \i -> do
putStrLn $ radianceToString (image V.! i)
else do
let pixels = V.map (radianceToRgb scr) image
forM_ [0..(V.length pixels - 1)] $ \i -> do
rgb <- smooth tracer scr pixels i
putStrLn $ rgbToString rgb
ここで出力される形式の画像フォーマットは無いが、あとで集計できるように一旦書き出 すだけなので拘らない。なお、結果を輝度値で出力することになると、従来の「エセ」ア ンチエリアシングがうまく働かなくなる。隣り合う画素のRGB値の差でアンチエリアシン グ処理を行うかどうかを判断していたからだ。これについては後で触れよう。
-2. 評価
■ フォトン数を一定にしたとき
フォトンマッピング法の生成画像の品質はフォトン数による。そこで、総フォトン数を 500万個に固定しイテレーションのフォトン数を変えて比較してみた。
| フォトン数 | イテレーション数 | 処理時間(s) | 処理時間(s)/イテレーション | メモリ量(MB)/イテレーション | 生成画像 |
|---|---|---|---|---|---|
| 10,000 | 500 | 3,632 | 7.27 | 65 |  |
| 50,000 | 100 | 1,034 | 10.34 | 120 |  |
| 100,000 | 50 | 835 | 16.70 | 169 |  |
| 200,000 | 25 | 875 | 34.99 | 359 |  |
| 500,000 | 10 | 1,661 | 166.05 | 360 |  |
そうフォトン数が同じでも処理時間と品質には結構ばらつきが出た。このシーンについて は、フォトン数100,000個が最もバランスが取れているように見える。フォトン数が 10,000個程度と少ない場合でもある程度のオーバーヘッドがあるようで、1回のイテレー ションに掛かる時間は劇的に短いわけではないようだ。
品質面ではちょっと微妙だった。画像を見比べてもあまりわからないかもしれないが、イ テレーション回数が多いと右下の集光模様の縁の鋭さがだいぶ違う。10,000個・500イテ レーションが最も良い。ただ、色の滲みは一番ざらざらした感じである。一方、100,000 個以上だと、滲みはほとんど違いがないので、縁の鋭さと処理時間を考えると200,000個 以上にする意味はほぼないと思われる。
■ イテレーション回数を一定にしたとき
次にイテレーション回数を100に固定して比較した。
| フォトン数/イテレーション | 処理時間(s) | 処理時間(s)/イテレーション | 処理時間(ms)/フォトン | 生成画像 |
|---|---|---|---|---|
| 1,000 | 552 | 5.52 | 5.52 |  |
| 5,000 | 619 | 6.19 | 1.24 |  |
| 10,000 | 669 | 6.69 | 0.67 |  |
| 50,000 | 1,034 | 10.34 | 0.21 |  |
| 100,000 | 1,508 | 15.08 | 0.15 |  |
| 200,000 | 3,407 | 34.07 | 0.17 |  |
当然の結果だが、同一回数のイテレーションならイテレーション毎のフォトン数が多い方 が品質が良いに決まっている。ただ、闇雲に増やすとメモリも時間も掛かりすぎる。ここ でも100,000個以上になると品質的にはほぼ変わらないように見える。放射輝度推定に使 うフォトンはkd木から検索する。アルゴリズムとしては計算量が O(n log n)になるらし いのでnが10,000以上になってくると処理時間はほぼnに比例するように思えるのだが、実 際には指数関数的に処理時間が掛かるようだ。フォトン数100,000個まではオーバーヘッ ドのためかあまり時間差は無いが、それを超えると処理時間が急増する。ちなみに1回あ たりフォトン数500万個で計算しようとしたら6時間経っても1イテレーションが完了しな いので中断した。今回のアルゴリズムでは参照半径が決まっているため、フォトンが多い ほどその領域に含まれるフォトンが多くなるわけで、一個のフォトンを検索する計算量x フォトン数増加量の時間が掛かることが一因ではと思う。
■ 並列処理
今回は統合処理をRubyで書いたが、並列処理(マルチスレッド)もRubyで行った。結論か らいうとあまり効果が出なかった。RubyではマルチスレッドにしてもCPU処理は直列に実 行されるらしい。
フォトン数100,000個、500イテレーションでマルチスレッド数を変えて時間を計測した。
| 並列度 | 1 | 2 | 4 | 10 |
|---|---|---|---|---|
| 処理時間(s) | 835 | 757 | 637 | 664 |
使用したPCは4コアなので、I/Oがある程度並列に実行されたのか並列度4までは若干時間 短縮がはかれているが、それ以上だと逆にオーバーヘッドが大きくなるようだ。
-3. OpenEXR対応
先日図書館で"[digital] ライティング&レンダリング 第3版"という本を見つけたので読 んでいたらいろいろ知らないことが書いてあったのだが、そこに High Dynamic Range Image (HDRI) の説明が あった。従来はRGB計24bitで画像データを保管してきたが、画像生成時は輝度を計算している。 上記の通りPPM-PAのためにわざわざ輝度値(浮動小数点数)で出力するように変えたのだから、 せっかくならそのまま保管できた方が活用の幅が広がる。そこで、最終結果はPPMだけでなくOpenEXR 形式でも保管できるようにした。util/averager2.rbがそれである。ファイル形式の詳細は以下の URLに詳しく書いてある。
特に最後にサンプルデータが説明されているのだが、バイト列とその意味が全部記載されており大いに参考になった。 ひとまずこの形式のデータが作れれば良いので、Single-Part、非圧縮、チャネルはRGB3色のみ、 各色は単精度浮動小数点数(32bit)とした。ファイルサイズが大きくなるのでは?とも思ったが、 PPMでも各色が3桁の数字だと1ピクセルあたり12バイト、OpenEXRでも先の条件なら12バイトなので それ程の差はない。実際、256x256解像度のファイルだと約791KBである。ちなみにImageMagickで JPEGに変換してみると約17KBになった・・・。
なおOpenEXRで保存しておくと、あとで露出などを簡単に変えられてなかなか楽しいこともわかった。
3. PPM-PAの応用
PPM-PAの直接的なメリットは、レンダリング時のメモリ使用量を抑え、かつフォトンマッピング法に 特有の色の滲みとぼやけを同時に緩和できることであると思う。しかし、独立したイテレーションを数百、 数千回繰り返すアルゴリズムなので、副次的に次の効果も容易に実装できるのが強みである。
今回はアンチエリアシングを(簡単だが)実装したので書いておく。
■ anti-aliasing
最初に書いたように、PPM-PA法を実現するために従来のアンチエリアシング処理は諦めざるをえなく なったが、多数のイテレーションを行うことでより良い(本当の?)アンチエリアシングが可能になった。 従来と今回の実装の違いは下図のとおり。
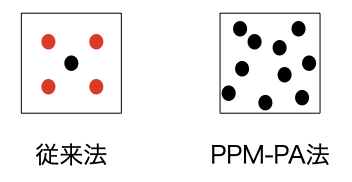
従来(左)は一度レンダリングした後の「追加処理」だったので 追加するレイ(赤丸)を4つだけにし、レイの方向も偏らないようあえて固定した。 PPM-PA(右)では100回、1000回とイテレーションを行うので、ランダムにレイを飛ばしても偏りは少ない だろう。
また、PPM-PAでのアンチエリアシングは「追加処理」ではないので計算コストが増えないのも大きな メリットである。イテレーション毎にレイの方向をランダムにずらしてあげれば良いのだ。 ということで、実装も非常に簡単である。ここでr3,r4は画素の中心からのx,y座標のずれ具合 (-0.5 〜 0.5)である。
(r3, r4) <- if prflag == True && aaflag == True
then do
r3' <- MT.randomIO :: IO Double
r4' <- MT.randomIO :: IO Double
return (r3' - 0.5, r4' - 0.5)
else
return (0.0, 0.0)
if文で"prflag == True"はPPM-PAを使うこと、"aaflag == True"はアンチエリアシングを行うことを 意味している。どちらかの フラグがFalseの場合はずらさないので0.0を返す。やることはたったこれだけである。
効果のほどは下の画像で比べてみればよくわかる。左がアンチエリアシングなし、右がありだ。 右の方は球の上部や天井からの光の斜めになっている境界のギザギザ(ジャギー)が緩和されている のがわかる。計算コストが増えないので、もうこれからはアンチエリアシングありだけで良いだろう。 (画像は解像度256x256、イテレーション500回、1回あたり100000フォトン)
| アンチエリアシング無し | アンチエリアシング有り |
|---|---|
 |
 |
4. まとめ
2年以上ぶりの記事となった。その間細かい変更をいくつかやっていて、記事にまとめておかないと 備忘録にならないので書いてみたが、今回の記事はほとんど実装面での説明がなく面白味がないかも しれない。ただ、3で挙げたいくつかの重要な「ボケ」などの効果・レンダリング処理のための布石としては 取り組んでよかったと思う。次はこれらの効果を追加していこう。
レイトレーシング(12): 集光模様!
0. 以前の記事の訂正
第8回の記事で完全拡散反射の場合のBRDF($f_r$)を下記のように示した。
が、間違いだった。shocker-0x15 さんからご指摘をいただきました。 ありがとうございます。正しい式は以下。
これにより、得られる輝度が全体的にほぼ倍になるが、輝度を画面の 色に変換するところで調整してやればいいので大きな問題はなかった。 やれやれ。
1. 今回の改善
今回は例トレーシング回の最終回ということで、やっと目標だった集光 模様の実現に取り組むことにする。また、ついでに球以外の形状の サポート、設定ファイルの対応もやってみた。
-1. Material型
まず最初にMaterial型の拡張について説明したい。Material型は
物体の物性や模様を表すために定義した型だ。前回までは単純な
完全拡散面を想定していたためパラメータは少ししかなかった(コード
自体には書いていても使っていないものもあった)。鏡面反射・屈折を
サポートするにあたりいくつかのパラメータを追加したし、実際に
値を使うようにコードを拡張した。下表に従来と今回の対応を示す。
| parameter | 型 | 説明 | 前回版 | 今回 |
|---|---|---|---|---|
| emittance | Radiance | 自己発光強度 | ○ | ○ |
| reflectance | Color | 拡散反射率(≒物体色?) | ○ | ○ |
| specularRefl | Color | 鏡面反射率(金属反射) | - | ○ |
| transmittance | Color | 透過率 | - | - |
| ior | Color | 屈折率 | - | ○ |
| diffuseness | Double | 拡散度※1 | ○ | ○ |
| metalness | Double | 金属性※2 | - | ○ |
| smoothness | Double | 平滑度 | - | - |
※1: 拡散反射と鏡面反射のあり合いを表す。1.0だと完全拡散反射、0.0 だと完全鏡面反射となる。鏡面反射方向からの光をどれだけ反射するか。
※2: 金属性と書いたが金属反射と透過の割合を表す。1.0だと完全に 不透明で金属反射のみ、0.0だとガラスのような透明物体となる。
なお、まだ対応できていないパラメータもある。transmittanceは透明物質内での
光の通過割合で、色ガラスのような物体を表すため、smoothnessは表面のざらつき
具合でぼやけたハイライトなどを表すためのパラメータだ。ぜひともこれらも実装
したいが、今後の課題とする。
iorの型がColorになっているのは、色(光の波長)毎に屈折率が違う
場合があるため。三角プリズムによる光の分散を再現するために必要だ。
(とはいえ、現状は赤、緑、青の3波長しか扱っていないため、いわゆる虹色に
ならないが)
各パラメータがどのように使われるかは後の節で説明する。
-2. 鏡面反射・屈折ベクトル
反射・屈折ベクトルの求め方については、いろいろなところに情報があるので ここでは割愛し、数式とコードのみ示すことにしよう。各記号・文字がわかり 易いように、全体を図にするとこんな感じ。

(反射)
入射ベクトル 、法線ベクトル $\boldsymbol{n}$ とする時、求める反射ベクトル
$\boldsymbol{v_r}$ は、
である。ただし、$\boldsymbol{e}, \boldsymbol{n}$ は正規化(=長さが1)されているものとする。 コードは次の通り。
specularReflection :: Direction3 -> Direction3 -> (Direction3, Double) specularReflection n e | v == Nothing = (n, 0.0) | c < 0.0 = (fromJust v, -c) | otherwise = (fromJust v, c) where c = e <.> n v = normalize (e - (2.0 * c) *> n)
まあ、コードは上式をそのまま表現しただけである。戻り値は反射ベクトルの他に 内積 $\langle \boldsymbol{e}, \boldsymbol{n} \rangle$ すなわち $\cos \theta$ ( $\theta$ は $\boldsymbol{e}$ と $\boldsymbol{n}$ のなす角) も含めている。$\cos \theta$ は あとで使われることが多いのだ。
(屈折)
絶対屈折率 の物質から絶対屈折率
の物質に光が入射した場合、
入射角
に対し、屈折ベクトルの角度が法線に対して
とすると
それらの間には以下の関係が成り立つという(理屈はよくわかっていない)。
この関係式を使うと、(途中の式変形などはよくわからないが)屈折ベクトル $\boldsymbol{v_t}$ は次の式で求められる。
ここで $\cos \theta$ は反射のときと同じ。コードは下記のとおり。
specularRefraction :: Double -> Double -> Double -> Direction3 -> Direction3 -> (Direction3, Double) specularRefraction ior0 ior1 c0 ed n | r < 0.0 = (o3, 0.0) | t == Nothing = (o3, 0.0) | otherwise = (fromJust t, ior') where ior' = ior0 / ior1 r = 1.0 / (ior' * ior') + c0 * c0 - 1.0 a = c0 - sqrt r n' = if ed <.> n > 0.0 then negate n else n t = normalize (ior' *> (ed + a *> n'))
引数のior0、ior1、c0は数字が紛らわしいが、それぞれ 、
、 $\cos \theta$ を意味する。
edは入射ベクトル $\boldsymbol{e}$ である。where節を
少し説明しよう。屈折ベクトルを求める式中に平方根が含まれている。この中身が
マイナスになる場合、光は全反射する(=屈折ベクトルは存在しない)。
これをチェックするため、一旦平方根の中身をrとし、ガードでマイナスの場合は
零ベクトルを返している。さて、屈折ベクトルを求めるには入射光が通ってきたのと
同じ側に向いた法線ベクトルが必要だが、本プログラムでは交点での法線は常に物体の
「外側」に向くよう定義している。つまり球なら表面から外側に法線ベクトルが向く。
しかし屈折では物体内部を光が通って物体表面にて反射と屈折が起きる。
この場合、反射屈折ベクトルの計算に必要なのは物体の内側に向いた法線ベクトルである。
そのためわざわざ $ \cos \theta $ の符号をみて $\boldsymbol{n}$ を反転させている(n')。
このことは屈折だけでなく反射も同じだが、ガードによる条件分岐で済ましている。
あとは上述の数式通りなので特に問題ないだろう。屈折はおまけとして比屈折率
( )も戻り値に入れている。
(Schlickの近似式)
鏡面反射・屈折では、物体表面の反射率が入射角により変化する。正確には Fresnelの公式というので求めるのだが、これがなかなかややこしい。おそらく計算 負荷も高い。そこで便利な"Schlickの近似式"というのを代わりに使うそうだ。
ここで、$F_0$ は物質の法線方向からの光の反射率である。物質によりその 値が異なる。上記近似式とともに、下記のWebページにいくつかサンプルがある。
https://ja.wikipedia.org/wiki/フレネルの式 http://d.hatena.ne.jp/hanecci/20130525/p3 https://yokotakenji.me/log/math/4501/
ここで、上述の鏡面反射ベクトル計算で返される $ \cos \theta $ が必要なのだ。
コードはこちら。$ F_0 $ (Color型)と $ \cos \theta $ が引数である。
あとは上記の近似式そのままだ。
reflectionIndex :: Color -> Double -> Color reflectionIndex (Color r g b) c = Color (r + (1-r) * c') (g + (1-g) * c') (b + (1-b) * c') where c' = (1.0 - c) ** 5.0
-3. フォトン追跡
鏡面反射・屈折が追加されたので、フォトン追跡もそれに合わせて いろいろ拡張せねばなるまい。これまでは拡散面だけだったので、 その反射率によって拡散反射か吸収(つまり追跡終了)しかなかったが、 フォトン追跡の条件分岐のバリエーションが増えた。
- 拡散反射か鏡面反射か吸収か
- 反射か屈折か
この場合分けを前述のMaterialの各パラメータとロシアンルーレットを
使って表現していくのだ。解り易いようにフローチャートで表そう。
下図に前回(拡散反射面だけ)と今回(鏡面反射・屈折追加)のフローを示そう。
前回のフローは今回のフローの一部になっている(赤点線の部分)のだ。

次にコードで比べてみる。前回のコードはこちら。
tracePhoton :: [Object] -> Int -> Photon -> IO [PhotonCache] tracePhoton os l (wl, r) = do let is = calcIntersection r os if is == Nothing then return [] else do let (p, n, m) = fromJust is i <- russianRoulette wl [reflectance m] pcs <- if i > 0 then reflect p n os l wl else return [] if (useClassicForDirect == False || l > 0) && diffuseness m > 0.0 then return $ ((wl, initRay p (getDir r)) : pcs) else return pcs
中程のrussianRouletteにて拡散反射率による分岐をしている。関数reflectは
拡散反射してさらにフォトンを追跡するものだ。最後のifは前回取り入れた
画質向上策である。
一方、今回拡張したコードはこちら。
tracePhoton :: Bool -> Material -> [Object] -> Int -> Photon -> IO [PhotonCache] tracePhoton _ _ _ 10 _ = return [] tracePhoton !uc !m0 !os !l !(wl, r) | is == Nothing = return [] | otherwise = do let is' = fromJust is (p, _, m) = is' d = diffuseness m i <- russianRoulette [d] ref <- if i > 0 then reflectDiff uc m0 os l wl is' else reflectSpec uc m0 os l (wl, r) is' if (uc == False || l > 0) && d > 0.0 then return $ ((wl, initRay p $ getDir r) : ref) else return ref where is = calcIntersection r os reflectDiff :: Bool -> Material -> [Object] -> Int -> Wavelength -> Intersection -> IO [PhotonCache] reflectDiff uc m0 os l wl (p, n, m) = do i <- russianRoulette [selectWavelength wl $ reflectance m] if i > 0 then do -- diffuse reflection dr <- diffuseReflection n tracePhoton uc m0 os (l+1) $ (wl, initRay p dr) else return [] -- absorption reflectSpec :: Bool -> Material -> [Object] -> Int -> Photon -> Intersection -> IO [PhotonCache] reflectSpec uc m0 os l (wl, (_, ed)) (p, n, m) = do let f0 = selectWavelength wl $ specularRefl m (rdir, cos0) = specularReflection n ed f' = f0 + (1.0 - f0) * (1.0 - cos0) ** 5.0 j <- russianRoulette [f'] if j > 0 then tracePhoton uc m0 os (l+1) (wl, initRay p rdir) else do if (selectWavelength wl $ ior m) == 0.0 then return [] -- non transparency else reflectTrans uc m0 os l wl ed (p, n, m) cos0 reflectTrans :: Bool -> Material -> [Object] -> Int -> Wavelength -> Direction3 -> Intersection -> Double -> IO [PhotonCache] reflectTrans uc m0 os l wl ed (p, n, m) c0 = do let ior0 = selectWavelength wl $ ior m0 ior1 = selectWavelength wl $ ior m (tdir, ior') = specularRefraction ior0 ior1 c0 ed n m0' = if tdir <.> n < 0.0 then m else m_air tracePhoton uc m0' os (l+1) (wl, initRay p tdir)
一見して前回と比べてかなり複雑になったのがわかるだろう。russianRouletteが
いくつか使われており、それが各分岐になっている。reflectDiff, reflectSpec,
reflectTransはそれぞれ拡散反射、鏡面反射、屈折の場合のフォトン追跡の処理だ。
屈折をサポートしたので、最初の目的だった「集光模様」が得られる はずだ!というわけで、ガラス球を配置してフォトンマップを生成してみよう。

左が不透明な拡散反射面の球の場合、右がガラス球だ。左は拡散反射するので 球の形にフォトンが記録されていて下に球の影が見える。一方右はガラス球 なので球面状にフォトンは記録されず、代わりに球の影の真ん中にフォトンが 集中している部分がある。これが集光模様になるのだ!
-4. レンダリング方程式(?)
さて、いよいよレンダリングの拡張だ。フォトンマップをみる限り、想定したとおり 集光模様が描けそうな気がする!
レンダリングは、注目する点(視線レイと物体の交点)にいろいろな方向から届く 光を集計して輝度として返せば良い。ただ、言葉では簡単だがこれがなかなか難しい。 私はいまだに良い(正確な/物理的に正しい/表現力の高い/…)集計方法がわからない。 とはいえわからないなりに作るしかないので、今回採用した集計方法を説明しよう。
まずは前回までの式。
各文字はそれぞれ以下を表す。
- $L_o$ : 交点から視線方向への輝度
- $L_e$ : 物体の発光輝度
- $L_l$ : 光源からの直接光(フォトンマップから推定することも可)
- $L_d$ : 間接光(フォトンマップから推定)
- $d$ : 拡散度(
Material中のdiffuseness)
これだとそんなに複雑ではない。該当するコードは次の通り。
traceRay :: Int -> Double -> KT.KdTree Double PhotonInfo -> [Object] -> [Light] -> Ray -> IO Radiance traceRay 10 _ _ _ _ _ = return radiance0 traceRay l pw pmap objs lgts r | is == Nothing = return radiance0 | otherwise = return (em + di + ii) where is = calcIntersection r objs (p, n, m) = fromJust is em = sr_half *> emittance m di = if useClassicForDirect then brdf m $ foldl (+) radiance0 $ map (getRadianceFromLight objs p n) lgts else radiance0 ii = estimateRadiance pw pmap (p, n, m)
emが $L_e$ 、diが $L_l$ 、iiが $L_d$に相当する。直接光と間接光は
別々にBRDFを適用しているのでちょっとわかりにくいが、基本的に上記の式を
そのまま適用している。
鏡面反射と屈折が追加されたことで、輝度計算式は次のように拡張した。
各文字はそれぞれ以下を表す。
- $L_o$ : 交点から視線方向への輝度
- $L_e$ : 物体の発光輝度
- $L_l$ : 光源からの直接光(フォトンマップから推定することも可)
- $L_d$ : 間接光(フォトンマップから推定)
- $L_s$ : 鏡面反射方向の輝度
- $L_t$ : 屈折方向の輝度
- $d$ : 拡散度(
Material中のdiffuseness) - $f$ : 交点の反射率 (Schlickの近似式で計算)
- $ m $ : 金属性(
Material中のmetalness)
なお、$ d, f, m $ はいずれも $ 0 \sim 1 $の間の値をとる。コードは次の通り。 (そういえば物体の発光輝度に $\frac{1}{2 \pi}$ を掛けているのはなぜだっけ?)
traceRay :: Screen -> Material -> Int -> PhotonMap -> [Object] -> [Light] -> Ray -> IO Radiance traceRay _ _ 10 _ _ _ _ = return radiance0 traceRay !scr !m0 !l !pmap !objs !lgts !r | is == Nothing = return radiance0 | otherwise = do si <- if df == 1.0 || f == black then return radiance0 else traceRay scr m0 (l+1) pmap objs lgts (initRay p rdir) ti <- if f' == black || ior1 == 0.0 then return radiance0 else do let ior0 = averageIor m0 (tdir, ior') = specularRefraction ior0 ior1 cos0 (getDir r) n m0' = if tdir <.> n < 0.0 then m else m_air traceRay scr m0' (l+1) pmap objs lgts (initRay p tdir) return (sr_half *> emittance m + df *> brdf m (di + ii) + (1.0 - df) *> (f <**> si + (1.0 - mt) *> f' <**> ti)) where is = calcIntersection r objs (p, n, m) = fromJust is di = if useClassicForDirect scr then foldl (+) radiance0 $ map (getRadianceFromLight objs p n) lgts else radiance0 ii = estimateRadiance scr pmap (p, n, m) (rdir, cos0) = specularReflection n (getDir r) df = diffuseness m mt = metalness m f = reflectionIndex (specularRefl m) cos0 f' = negateColor f -- this means '1 - f' ior1 = averageIor m
反射屈折方向にトレースするかどうかの判定など多少ややこしい部分はあるが、 基本的には上記式をそのまま再現している。
さて、それでは拡張した今回のプログラムで数種類の物質の球をレンダリング してみよう。

鏡面反射が加わったことで、かなり表現力が高まった気がする。また、ガラス球が 表現できるようになり念願の集光模様が再現できた!
-5. おまけ:設定ファイルに対応
実はこれまではレンダリングする画像の情報(スクリーン情報と物体の情報)は ソースコードに直書きしていた。流石にシーンを変更するたびにソースを修正して リコンパイルするのは面倒臭く、またさまざまなシーンを描画するために画像情報を 残しておきたいことから、設定ファイルから情報を読み込むように改めた。
まずスクリーン情報(カメラの位置や向き、解像度、アンチエリアス要否など)を 表すファイル(Screenファイル)の例。フォーマットは(エセ)YAMLとした。
nphoton : 100000 xresolution : 256 yresolution : 256 antialias : yes # yes or no samplephoton : 100 useclassic : yes # yes or no estimateradius: 0.3 ambient : [ 0.001, 0.001, 0.001 ] maxradiance : 0.01 eyeposition : [ 0.0, 2.0, -4.5 ] targetposition: [ 0.0, 2.0, 0.0 ] upperdirection: [ 0.0, 1.0, 0.0 ] focus : 2.7 photonfilter : none # cone, gauss
こちらは単純な変数名と値の組だけなのでなんのことはない。一方シーン情報 (物体の形や配置、色などを定義)の例としてガラス球の場合を示そう。 ちょっと長いが勘弁願いたい。
light:
- type : parallelogram
color : [ 1.0, 1.0, 1.0 ]
flux : 5.0
position : [ -0.5, 3.99, 2.5 ]
dir1 : [ 1.0, 0.0, 0.0 ]
dir2 : [ 0.0, 0.0, 1.0 ]
material:
- type : solid
name : mwall
emittance : [ 0.0, 0.0, 0.0 ]
reflectance : [ 0.5, 0.5, 0.5 ]
transmittance: [ 0.0, 0.0, 0.0 ]
specularrefl : [ 0.8, 0.8, 0.8 ]
ior : [ 0.0, 0.0, 0.0 ]
diffuseness : 1.0
metalness : 0.0
smoothness : 0.0
- type : solid
name : mwallr
emittance: [ 0.0, 0.0, 0.0 ]
reflectance: [ 0.4, 0.1, 0.1 ]
transmittance: [ 0.0, 0.0, 0.0 ]
specularrefl: [ 0.0, 0.0, 0.0 ]
ior: [ 0.0, 0.0, 0.0 ]
diffuseness: 1.0
metalness: 0.0
smoothness: 0.0
- type : solid
name: mwallb
emittance: [ 0.0, 0.0, 0.0 ]
reflectance: [ 0.1, 0.1, 0.4 ]
transmittance: [ 0.0, 0.0, 0.0 ]
specularrefl: [ 0.0, 0.0, 0.0 ]
ior: [ 0.0, 0.0, 0.0 ]
diffuseness: 1.0
metalness: 0.0
smoothness: 0.0
- type : solid
name: mparal
emittance: [ 0.7958, 0.7958, 0.7958 ]
reflectance: [ 0.0, 0.0, 0.0 ]
transmittance: [ 0.0, 0.0, 0.0 ]
specularrefl: [ 0.0, 0.0, 0.0 ]
ior: [ 0.0, 0.0, 0.0 ]
diffuseness: 0.0
metalness: 0.0
smoothness: 0.0
- type : solid
name : glass
emittance: [ 0.0, 0.0, 0.0 ]
reflectance: [ 0.0, 0.0, 0.0 ]
transmittance: [ 0.0, 0.0, 0.0 ]
specularrefl: [ 0.08, 0.08, 0.08 ]
ior: [ 1.5, 1.5, 1.5 ]
diffuseness: 0.0
metalness: 0.0
smoothness: 0.0
vertex:
- cl01 : [ -0.5, 3.99, 2.5 ]
- cl02 : [ 0.5, 3.99, 2.5 ]
- cl03 : [ -0.5, 3.99, 3.5 ]
object:
- type : plain
name : flooring
normal : [ 0.0, 1.0, 0.0 ]
position: [ 0.0, 0.0, 0.0 ]
material: mwall
- type : plain
name : ceiling
normal : [ 0.0, -1.0, 0.0 ]
position: [ 0.0, 4.0, 0.0 ]
material: mwall
- type : plain
name : rsidewall
normal : [ -1.0, 0.0, 0.0 ]
position: [ 2.0, 0.0, 0.0 ]
material: mwallb
- type : plain
name : lsidewall
normal : [ 1.0, 0.0, 0.0 ]
position: [ -2.0, 0.0, 0.0 ]
material: mwallr
- type : plain
name : backwall
normal : [ 0.0, 0.0, 1.0 ]
position: [ 0.0, 0.0, -6.0 ]
material: mwall
- type : plain
name : frontwall
normal : [ 0.0, 0.0, -1.0 ]
position: [ 0.0, 0.0, 5.0 ]
material: mwall
- type : sphere
name : ball_glass
center : [ 0.0, 0.8, 3.0 ]
radius : 0.8
material: glass
- type : parallelogram
name : ceiling_light
pos1 : cl01
pos2 : cl02
pos3 : cl03
material: mparal
以前、CPU回で使ったParsecライブラリをここでも使ってみた。
CPU回でなんとなくパーサの感触をつかんでいたのであまりハマることなく
実装できた。Parsecを使ったパーサ作りは、乗ってくるとどんどん
パーサを高度化していけるので楽ちんだ。先人に感謝。
実行方法は次の通り(ガラス球の例、ex-11.6)。
$ cabal build $ dist/build/pm/pm example/screen0.scr example/ex-11.6.scene | dist/build/rt/rt example/screen0.scr example/ex-11.6.scene | convert - ~/tmp/ex-11.6.png
これで ~/tmp/ex-11.6.pngという画像ファイルが出来上がる。
ただ、同じ情報ファイルをフォトンマップ作成(pm)とレイトレーシング(rt)で
繰り返すのは面倒だし画像フォーマット変換(ImageMagickのconvertを使用)も
毎回書くのは邪魔臭いのでシェルスクリプトにすることにした。
$ util/drv.sh example/screen0.scr example/ex-11.6.scene ~/tmp/ex-11.6.png
2. 作例
上記の他にも少し作例を示そう。

左上は天井からの日光を鏡面三角柱で壁に反射している図、右上は例の フォトンマッピング本でなんども出てくる図。これがやりたかった! 下の二つは球以外の形状をガラスで作ってみたもの。最後に集光模様の 面白い例として光の波長により屈折率が異なるガラス球の画像。屈折率の違いに よりプリズムのように虹色(?)に分かれた集光模様になる。ただし、本プログラムは RGB三種類のフォトンしか使っていないため、青より短波長の紫が表現できない。 そこまでやるにはRGBに紫を追加してフォトンの種類を増やして追跡しないとだめ だろう。ちょっと面倒なので宿題にしておこう。

3. まとめ
今回でやっと集光模様までたどり着いた。最初Haskellでフォトンマッピングによる レイトレーシングプログラムに取り掛かった頃は正直自信がなかったが 数年がかりでここまできた。やれやれ。まあ、レイトレーシング・ツールとしては まだまだやることは大量にあるが、一旦ここまで。気が向いたら拡張しようと思う。
※ 今回分のソースはこちら。
レイトレーシング(11): 画質向上策2点
今回は寄り道
前回から半年も経ってしまった orz
前回で完全拡散面の反射まで実装した。当然次は鏡面反射、と思われたら 申し訳ないところだが、反射(と屈折)は手間がかかるので後回し。 今回は寄り道として生成画像の画質改善に取り組む。
1. 直接光は古典レイトレーシングで
フォトンマッピングでは、放射するフォトン数に限界があり、多数のフォトン から輝度推定しても"まだら模様"のようになってしまう。また、点光源では本来 影の縁はくっきりするものだが、残念ながらぼやけてしまう。
例の本(フォトンマッピング、Herik Wann Jensen、オーム社)では、 実践的なアルゴリズムとして「直接光はフォトンマップから推定するのではなく 古典レイトレーシングで」と書いてある(ようだ)。
確かにランダムなフォトンから推定するより数式できっちり計算できる 古典レイトレーシングを用いたほうが画質的には有利だろう。
前回までで、フォトンマッピング法の画像と比較するため古典レイトレーシングも 実装してきた。これをそのまま流用すればよい。基本的な考え方は次の通り。
- フォトン追跡では、光源から放射された直後のフォトンはマップに記録せず、 次の反射フォトンから記録するようにする(一次フォトンの記録は捨てる)。
- レイトレーシングでは、光源から直接届く光は数式から求め、それ以外の 間接光はフォトンマップから推定する。
実装
ではまずフォトン追跡の実装から。
tracePhoton :: [Object] -> Int -> Photon -> IO [PhotonCache] tracePhoton os l (wl, r) = do let is = calcIntersection r os if is == Nothing then return [] else do let (p, n, m) = fromJust is i <- russianRoulette wl [reflectance m] pcs <- if i > 0 then reflect p n os l wl else return [] if (useClassicForDirect == False || l > 0) && diffuseness m > 0.0 then return $ ((wl, initRay p (getDir r)) : pcs) else return pcs
tracePhotonに$l$という第二引数を設けている。これは追跡の深さを
表すもので、物体に当たって反射するたびに1ずつ増やして反射方向の追跡を
するようにした。つまり$l=0$ならまだ反射していないから「光源からの
直接光」である。
if (useClassicForDirect == False || l > 0) && diffuseness m > 0.0
これがその判定をしているところ。
useClassicForDirectは、光源からの直接光を古典レイトレーシングで計算 するかどうかのフラグ。Falseはこれまでどおりフォトンマップから推定する という意味。l > 0は前述の通り一回以上反射したフォトンを意味する。diffuseness m > 0.0はフォトンが衝突した物体表面が、少しでも 拡散反射の要素を持っている=フォトンを記録する必要があるという意味。
これらのいずれにも合致しない場合は、そのフォトンの衝突点ではフォトンマップに 記録しない。
次にレイトレーシング部分を見てみよう。
traceRay :: Int -> Double -> KT.KdTree Double PhotonInfo -> [Object] -> [Light] -> Ray -> IO Radiance traceRay 10 _ _ _ _ _ = return radiance0 traceRay l pw pmap objs lgts r | is == Nothing = return radiance0 | otherwise = return (em + di + ii) where is = calcIntersection r objs (p, n, m) = fromJust is em = sr_half *> emittance m di = if useClassicForDirect then brdf m $ foldl (+) radiance0 $ map (getRadianceFromLight objs p n) lg ts else radiance0 ii = estimateRadiance pw pmap (p, n, m)
where節の後半でuseClassicForDirectというフラグをチェックしている。
ここの仕組みはこうだ。
useClassicForDirectが真の場合は、物体上の点に注ぐ直接光を古典 レイトレーシングで計算する。getRadianceFromLight関数がそれ。光源の 数だけ繰り返している。偽の場合は、古典では輝度を計算しないので値ゼロ (=radiance0)としている。- その点には間接光も入ってくるので、その輝度は従来通りフォトンマップから
推定する。(ifの下の
estimateRadiance)
なおフォトンマップから求められる輝度は、古典レイトレーシングを使う場合には 「直接光のフォトンを記録しない」ようにしてあるので、ちゃんと間接的に注ぐ 光だけで輝度推定される。古典を使わない場合は直接光のフォトンも記録されて いるので従来と同じ結果となる。
画像比較
では生成された画像を比べてみる。まずは点光源の場合。

効果は一目瞭然だろう。直接光を古典で計算した場合(図2)は奥の壁、床、球の 上面が滲みなく滑らかに描画されている。直接光の当たらない天井や影の部分は 間接光が支配的なので致し方ないが。注目は球の影。従来はどうしても縁がぼやけて しまったがそこがくっきりしている。点光源はこうでないと。次に平面光源の場合。

こちらも同様にスムーズだ。最後に平行光源の場合。

図5は壁面の直接光の当たる境界がぼやけてしまっているが、古典を使うと くっきりしたエッジになっている。本来こうあるべきだ。 (こちらの画像の場合天窓からの光以外は全て間接光なので、ほとんどマダラが 残ったままだが、ここは我慢)
処理時間も比べてみよう。直接光を古典レイトレーシングに任せることで 直接光のフォトンを記録しないと書いた。つまりフォトンマップが小さく なるということだ。結果は次の表のとおり。
| 図 | 画像 | 直接光 | フォトン数 | 処理時間(MM:SS) |
|---|---|---|---|---|
| 1 | 点光源 | フォトンマップ | 318,164 | 6:50 |
| 2 | 点光源 | 古典レイトレ | 117,852 | 1:22 |
| 3 | 面光源 | フォトンマップ | 288,976 | 6:14 |
| 4 | 面光源 | 古典レイトレ | 89,420 | 1:09 |
| 5 | 平行光源 | フォトンマップ | 321,142 | 23:07 |
| 6 | 平行光源 | 古典レイトレ | 120,841 | 2:01 |
どうやらフォトンマップが小さいと輝度推定時にフォトン収集の時間が短くて 済むようで、圧倒的に処理時間が短くなることがわかった! 特に平行光源の例では1/10に短縮できている。なぜこれほど短縮できるのか (もしくはフォトンマップだけだと時間がかかるのか)はよくわからないが。
2. えせアンチエリアシング
もう一つの画質改善ネタであるアンチエリアシングに移ろう。 アンチエリアシングの詳しい説明はWebを漁れば山ほど出てくるのでそちらを 見ていただくとして、今回実装した仕組みを説明しよう。
仕組み
レイトレーシングは画面を格子状に分割し、その分割された小さい四角 (ピクセル)の中心に向かって光を逆向きに追跡する(追跡レイとする)。 各ピクセルの輝度値がある閾値を超えたら、そのピクセルの内側のいくつかの 点を追加で追跡し、その輝度を平均する。
節タイトルで「えせ」としたのは、ちゃんとアンチエリアシングしたければ 追加する追跡レイはピクセル内の「ランダム」な場所に対して行うべきだから である。規則的に追跡レイを追加するとどうしてもエリアシングの問題が 残るらしい。しかし今回は、小難しいことを考えるのがだるかったので実装の 簡便さを優先した。。。時間があったらちゃんと実装しよう。
まず、すべてのピクセルで追跡レイを追加していたら時間ばかりかかって非効率 なので追加すべきかどうかをまず判断する。そのため、とあるピクセル(p)とその 周りの8つのピクセルについてそれぞれ差を求め、閾値を超えているか判定する。 1点でも閾値を超えていたら追加レイを飛ばす。(下図)

なお、このプログラムでは差を求める際に輝度を比較するのではなくRGB値、 すなわち「画面に出力する色」に変換してから比較している。なぜなら、 結局目に見えるところでの色の違いがある場合に追加レイを飛ばしたいから。 最初は輝度で試したが、閾値の設定がシーンの明るさ・光の量で変える必要が あり設定が難しく、実用的でないと判断した。
次に追加レイを飛ばす場所だが、上記の通り規則的にした。ピクセル内の 中心以外の4点だ。単純にピクセルを4分割してそれぞれの中心点に向かって 追跡している。

これら4点と最初に計算した中心点の全5点から得られた輝度を平均するのだが、 その方法には単純平均するか重み付けするかがある。結果に微妙な差が出るが 大きな問題はないと判断し、今回は単純平均する。ランダムに追加レイを飛ばす 場合は中心からの距離に差が出ると思うのでちゃんと重み付けした方が よいだろう。
実装
アンチエリアシングを実施するかどうかはメインループの最後のところ。
: forM_ [0..(V.length pixels - 1)] $ \i -> do rgb <- smooth antiAliasing tracer pixels i putStrLn $ rgbToString rgb
smooth関数で処理している。引数のantiAliasingはアンチエリアシングを
実施するかどうかのフラグ。smoothは次の通り。
smooth :: Bool -> (Ray -> IO Radiance) -> V.Vector Rgb -> Int -> IO Rgb smooth False _ ims i = return (ims V.! i) smooth True tracer ims i | isDifferent i ims imgOffset == False = return (ims V.! i) | otherwise = do l <- retrace tracer i return $ avg ((ims V.! i):l)
まずフラグが偽なら何もせず最初に求めた色を返す。真の場合、まずは追跡レイを
追加するかどうか判断する(isDifferent)。追加が必要なければやはりそのまま
色を返す。追加が必要となったら再トレースだ(retrace)。そこで得られた色を
avgで平均して返せばOK。
追加が必要かどうかの判断は次の通り。
isDifferent :: Int -> V.Vector Rgb -> [Int] -> Bool isDifferent _ _ [] = False isDifferent p rs (i:is) | p' < 0 = isDifferent p rs is | p' >= length rs = isDifferent p rs is | df = True | otherwise = isDifferent p rs is where p' = p + i df = diffRgb (rs V.! p) (rs V.! p')
少し説明が必要かもしれない。2番目の引数は、すでに
計算済みの画面全部の色値(RGB)の配列(Vector)である。着目しているピクセルは
第一引数pに配列内の位置として与えられる。p'が比較対象となる
周りのピクセル(の位置)は、第3引数で与えられている。
これは上の方で次のように定義されている。
imgOffset :: [Int] imgOffset = [-xres-1, -xres, -xres+1, -1, 1, xres-1, xres, xres+1]
画面の横方向画素数xresを使い、着目点pに対するオフセットを
示しているわけだ。このようにして、周りの8個の点と比べ、閾値を
超えたら直ちにTrueを返すようにしてある。周りの点が画面をはみ出す
場合はもちろん無視だ(条件 p' < 0とp' >= length rs)。
次に再トレース部分を説明しよう。
retrace :: (Ray -> IO Radiance) -> Int -> IO [Rgb] retrace tracer p = do let p' = (fromIntegral (p `div` xres), fromIntegral (p `mod` xres)) ls <- mapM tracer $ map generateRay' (map (badd p') blur) return $ map radianceToRgb ls
といっても大したことはない。現在の着目点pに対し、1/4ずつずれた4点を
求め、それぞれ普通に追跡して結果をリストにして返しているだけだ。
ずれた点を計算しやすくするため、blurをあらかじめ定義している。
blur :: [(Double, Double)] blur = [(-0.25, -0.25), (-0.25, 0.25), ( 0.25, -0.25), ( 0.25, 0.25)]
生成画像の比較
では実際にアンチアリアスを効かせた画像を生成してみよう。従来の画像との 比較はつぎのとおり。


ぱっと見はよくわからないかもしれないが、特に球の上部や平面光源の縁が気持ち なだらかになったのがわかるだろうか?これがアンチエリアシングの効果だ。 ただ、いくつかのピクセルについて追加レイを飛ばすので、当然計算時間が 余計にかかる。
| アンチエリアシング | フォトン数 | 処理時間(MM:SS) |
|---|---|---|
| 無 | 89420 | 1:09 |
| 有 | 89420 | 1:52 |
画面の複雑さや色合いにもよるので一般にどのぐらい時間が増えるかは なんとも言えないが、この例ではほぼ2倍の計算時間がかかったことになる。 この辺は画質とのトレードオフだが、世間のCGソフトは普通アンチエリアシングが 効いているからなぁ。
まとめ
今回は多少なりとも画質を向上する策として、以下の2点の改善を実施した。
両方とも、簡便な方法を採った割にはそれなりにうまくいったと思う。 また、古典レイトレーシングを使うことで大幅な計算時間の短縮ができた ことは収穫だった。
次回はとうとう(?)鏡面反射、屈折に対応しよう。うまく行けばいわゆる 「集光模様」が得られるはずだ。
ここまでのソースはこちら。
レイトレーシング(10): 拡散反射と面光源
DeepLearning回からだいぶ間があき、さらにレイトレーシングは1年半以上も 時間が空いてしまった。それは拡散反射でとある処理の解法で壁にぶつかって いたからだ。それが非常に簡単に解決できるとわかったのでちょっと進める ことにした。
0. 前回まで
前回までで、フォトンマッピング法を用いたレイトレーシングプログラムを 作成した。といってもフォトン追跡は何か物体にぶつかったらそれでおしまい、 反射は未対応という中途半端な状態だ。
久しぶりなので気分を一新して新しいシーンに変えてみよう。 実はこのページのパクリだ。 ちなみにこの連載は知りたいことが多く書いてありとても参考にさせて いただいている。売り物の3DCGソフトを使っての説明だが理論的なところが 詳しくよくわかる。
さて、前回までで作ったフォトンマッピングプログラムと古典レイトレーシングで 描画したものがこちら。

一目瞭然、フォトンマッピングのほうは影がぼやけてしまう。 点光源なので影は古典のようにくっきりとした縁、かつ真っ黒でなければ ならない。前の記事でも書いたがフォトンマッピングはある点の周囲のフォトンを 集計して輝度を計算するので、影のなかにフォトンがないと収集する範囲を 広げてしまうのだ。
ということでさらの前回のおさらいだが、フォトンを収集する範囲を 限定して描画してみる。設定は0.2 [m]だ。それより外のフォトンは無視して 輝度を判定する。

残念ながら影の縁はぼやけてしまうが、上の画像よりははるかに本物っぽい。 今後はひとまずフォトンの収集範囲を0.2 [m]として、色々試すことにしよう。 ちなみにフォトン数は20万個、これでも残念ながら"まだら模様"になるのは 今は我慢しよう。
なおフォトンマッピングと古典レイトレーシングでは輝度の計算方法が全く 異なるわけだが、両者の明るさや色の加減はほぼ同等であることに注目したい。 レイトレーシングといっても要するに物理(光学)シミュレーションなので 同じ設定なら(ほぼ)同じ結果が出てこないといけないのだ。その点で、 ひとまず両者のプログラムに大きな間違いはなさそうだ。
1. 拡散反射の実装
さて本題の拡散反射である。現時点ではシーン中の全物体は完全拡散反射面 としているので、フォトンを追跡して物体にぶつかったらフォトンマップに 記録し、別方向へ反射させればよい。ところが長い間詰まっていたのは その反射方向をどうするか、であった。
(1) 拡散反射ベクトルの生成法
完全拡散反射面ではフォトンが物体にぶつかるとその面の半球状のいずれかに 等確率で反射する。当初は、まず上方向の平面を考え、半球のどこかへ向かう ベクトルを求めてからそれを法線方向によって回転させようとした。

反射ベクトルは点光源でフォトンをランダムに生成した経験から、それを 上半分だけに限定すれば生成できる。あとは回転だが、回転行列を作るのか四元数を 使うのか、よく分からないまま止まっていた。一般的にどうしているのか検索も してみたがどうもそれらしい情報を見つけられない。
で、先日極めて容易に生成できる方法に気がついた。球状のランダムなベクトルを 生成したあと、求めたい面の法線とのなす角が90度以下ならそのまま採用、90度 以上なら反転させればいいのだ。

なんと簡単なことに長時間悩んだことか、恥ずかしくなるぐらいだ。。。
この処理をコードにすると次の通り。generateRandomDir?は以前作って
いたもの(生成方法により四種類あり、?はその番号、一例として四番目を示す)。
generateRandomDir4 :: IO Direction3 generateRandomDir4 = do y' <- MT.randomIO :: IO Double p' <- MT.randomIO :: IO Double let y = y' * 2.0 - 1.0 p = p' * 2.0 * pi r = sqrt (1 - y * y) x = r * (cos p) z = r * (sin p) v = initPos x y z len = norm v return $ fromJust $ normalize v
diffuseReflectionが反射ベクトルの生成だ。
diffuseReflection :: Direction3 -> IO Direction3 diffuseReflection n = do d <- generateRandomDir4 let cos = n <.> d return $ if cos > 0.0 then d else negate d
こんなたった数行でできることに悩まされていたとは・・・。
(2) フォトン追跡をいじる
反射ベクトルを作ることができたので、フォトン追跡にも手を 入れよう。従来の追跡処理は次のようであった。
コードはこちら。
tracePhoton :: [Object] -> Photon -> IO [PhotonCache] tracePhoton os (wl, r) = do let iss = filter (\x -> fst x > nearly0) (concat $ map (calcDistance r) os) (t, s) = head $ sortBy (comparing fst) iss return [(wl, initRay (target t r) (getDir r))]
ここは大幅に変更している。やりたいことは次の通り。
- フォトンがぶつかる最初の物体との交点を得る(
calcIntersection) - ぶつからなければ空リストを返す。
- ロシアンルーレット法を使い物体の反射率以下なら反射(
reflect)し さらにフォトン追跡をしてPhotonCache情報を得る。 - 反射率以上ならフォトンが吸収されたとして追跡を止める。
- 交点が拡散反射面(*1)ならその点の
PhotonCahce情報を作成する。 - 交点および反射方向から全
PhotonCache情報を集めて返す。
(*1)について、今は拡散反射面という前提だが、将来の拡張のため このような判定を入れている。上記処理のコードは次の通り。
tracePhoton :: [Object] -> Int -> Photon -> IO [PhotonCache] tracePhoton os l (wl, r) = do let is = calcIntersection r os if is == Nothing then return [] else do let (p, n, m) = fromJust is i <- russianRoulette wl [reflectance m] pcs <- if i > 0 then reflect p n os l wl else return [] if diffuseness m > 0.0 then return $ ((wl, initRay p (getDir r)) : pcs) else return pcs reflect :: Position3 -> Direction3 -> [Object] -> Int -> Wavelength -> IO [PhotonCache] reflect p n os l wl = do dr <- diffuseReflection n let r' = initRay p dr pcs <- tracePhoton os (l+1) (wl, r') return pcs
なお、後々の拡張のため、反射回数を引数に追加している(l)。
ちなみにrussianRouleteはこのようになっている。
russianRoulette :: Wavelength -> [Color] -> IO Int russianRoulette wl cs = do r <- MT.randomIO :: IO Double return $ rr wl cs 0.0 r (length cs) rr :: Wavelength -> [Color] -> Double -> Double -> Int -> Int rr _ [] _ _ len = len rr wl (c:cs) c0 r len | r < c' = len | otherwise = rr wl cs c' r (len - 1) where c' = c0 + selWl wl c selWl :: Wavelength -> Color -> Double selWl Red (Color r _ _) = r selWl Green (Color _ g _) = g selWl Blue (Color _ _ b) = b
まず[0,1]の一様乱数rを作り、Colorのリストから指定の波長の値を取り出して
そのrを上回ったところでリスト要素の順番(逆順)を返す。
分かりにくいので例を示す。物質の反射率、透過率が次のようで
あったとする。ただし各色の反射率+透過率は1.0を超えない。
反射率: 赤=0.5、緑=0.1、青=0.6
透過率: 赤=0.2、緑=0.6、青=0.4
1.0-(反射率+透過率)は吸収率だ。ここで赤を例に判定しよう。その場合、
リスト[Color]は[[0.2,0.6,0.4],[0.5,0.1,0.6]]である。赤について取り出すと
[0.2,0.5]だ。rが0.6であれば、
- 1番目の透過率=0.2と比べると
rが大きいので次へ - 2番目の反射率=0.5だが先の0.2とあわせて0.7として
rと比較すると、 今度はrが小さいので、この時の要素数1を返す
ということで1になる。

もしrが0.1なら1番目の透過率0.2より小さいので結果は2なわけだ。この番号は、
先のフォトン追跡の際に吸収、反射、透過のどれかを表すのに使っており、
このプログラムでは0=吸収、1=反射、2=透過と決めた。なので、
russianRouletteの返値が0より大きければフォトンを反射してさらに追跡
するようにしている。
i <- russianRoulette wl [reflectance m] pcs <- if i > 0 :
さて、それでは次に画像を生成してみよう。
(3) 間接光の効果はすごい
拡散反射を実装したので、あらためてフォトンマップを生成する。
$ cabal build : $ dist/build/pm/pm > scene1.map $ dist/build/rt/rt < scene1.map > scene1.ppm
以下に、機能拡張したプログラムで生成した画像と比較のため直接光のみの 画像および古典版を示す。古典版はいわゆる「環境光」に2 [mW/m2/sr]の輝度を与えた。

結果は明らかだ。まだら模様と影の縁がぼやけているのは仕方ないとして、
- 球の下の方は床からの照り返しでほんのり明るくなっている
- 球の左右はそれぞれ赤・青の壁からの反射で少し赤み・青みがかっている
- 天井も壁からの照り返しがある
など、だいぶリアルな画像が得られたと思う。まだら模様もまあいわゆる 「味わい」と言えなくもない(と自分を慰めてみる)。
2. 面光源も
さて、拡散反射による間接光が思いの外いい効果を出したので、もう少し 拡張してみる。先の例では点光源なのに影の縁がぼやけていた。でも大きさの ある光源ならぼやけていて当たり前、違和感がないはず?
まずは実装が簡単そうな平面光源を追加してみる。
(1) 平面光源
点光源は一点から球状のあらゆる方向へフォトンが放射されるが、面光源は 面のそれぞれの点から半球状に放射される。そう、拡散反射の実装で拡散反射 ベクトルを求めたがそれがそのまま使える。あとは平面をどう定義するかだが、 あまり手をかけたくないので2つのベクトル($\boldsymbol{d_1}, \boldsymbol{d_2}$)で表される 「平行四辺形」にしたいと思う(下図)。

フォトンの放出方法だが、まず面光源のどこから放出されるかを2つの一様 乱数($0 \leq u \leq 1, 0 \leq v \leq 1$)で決める。放出点を $p$ とすると、
$ \boldsymbol{p} = \boldsymbol{p_0} + u \cdot \boldsymbol{d_1} + v \cdot \boldsymbol{d_2} $
となる。あとは拡散反射と同様に半球状のランダムな方向ベクトルを生成して フォトンを飛ばしてやれば良い。コードにするとこんな感じ。
data Light = PointLight { lcolor :: Color , lflux :: Flux , pos :: Position3 } | ParallelogramLight { lcolor :: Color , lflux :: Flux , pos :: Position3 , nvec :: Direction3 , dir1 :: Direction3 , dir2 :: Direction3 } generatePhoton (ParallelogramLight c _ p n d1 d2) = do wl <- MT.randomIO :: IO Double t1 <- MT.randomIO :: IO Double t2 <- MT.randomIO :: IO Double d <- diffuseReflection n let r = initRay (p + t1 *> d1 + t2 *> d2) d w = decideWavelength c wl return (w, r)
生成してみたフォトンマップがこちら。天井に黒い四角が見える。これが面光源。

さて、これを使ってレイトレーシングしたいのだが、問題は大きさのある光源の 場合「目に見える」ということだ。点光源は大きさがないので無視していたが、 今度はそうはいかない。なのでレイトレーシング時に他の物体と同じように 交差判定とかしてやらないといけない。というか本来は逆だ。物体がたまたま 光を放出しているから光源なのだ。というわけで、物体の表面属性に「発光」を 加えてやろう。他にも今後対応する(かもしれない)反射・透過関係も入れて、 次のように定義した。
data Material = Material { reflectance :: Color , transmittance :: Color , specularRefl :: Color -- specular reflectance , emittance :: Radiance , ior :: Color -- index of refraction , diffuseness :: Double -- 拡散性 , smoothness :: Double } deriving Eq
このemittanceがそれだ。ここまでくると、物体定義を使って
光源としての処理をしてやるのが筋ってもんだ、と思う。つまり
Light型を物体と別に定義するのではなく物体を使ってフォトン放出を
するということだ。が、ちょっと手間なので今回は割愛、今後のがんばりに期待。
で、代わりに「平行四辺形」という物体を定義してやろう。
data Shape = Point !Position3 | Plain !Direction3 !Double | Sphere !Position3 !Double | Parallelogram !Position3 !Direction3 !Direction3 !Direction3 deriving Eq
Parallelogramがそれ。あとは他の物体と同じく各関数を定義してやる。
getNormal p (Parallelogram _ n _ _) = Just n distance r@(pos, dir) (Parallelogram p n d1 d2) | res == Nothing = [] | otherwise = [t] where res = methodMoller 2.0 p d1 d2 pos dir (u, v, t) = fromJust res
ポリゴンの当たり判定はこのページを 参考にさせていただいた。「Tomas Mollerの交差判定」だそうだ。これを次のように 定義した。
methodMoller :: Double -> Position3 -> Direction3 -> Direction3 -> Position3 -> Direction3 -> Maybe (Double, Double, Double) methodMoller l p0 d1 d2 p d | detA == 0.0 = Nothing | u < 0.0 || u > 1.0 = Nothing | v < 0.0 || v > 1.0 = Nothing | u + v > l = Nothing | otherwise = Just (u, v, t) where re2 = d <*> d2 detA = re2 <.> d1 p' = p - p0 te1 = p' <*> d1 u = (re2 <.> p') / detA v = (te1 <.> d) / detA t = (te1 <.> d2) / detA
なお、もともとは三角ポリゴンの判定に使うもので、計算される $u$, $v$ は
を満たす必要がある。しかし今回は平行四辺形の当たり判定をしたいので、
$ 0 \leq u \leq 1, 0 \leq v \leq 1 $
$ u + v \leq 2 $
とした。そのため以下のように謎の"2.0"が入っているのだ。
res = methodMoller 2.0 p d1 d2 pos dir
さあ、準備は整った。画像を生成してみよう。
$ dist/build/pm/pm > scene2.map $ dist/build/rt/rt < scene2.map > scene2.ppm
生成された画像と同じシーンを古典で生成したもの、および点光源の 画像を並べてみる。

まあ正直なところこの程度の平面光源では点光源と大差ないのだが。
(2) 平行光源=太陽光
このまま勢いに乗って平行光源に手を出そう! 典型的な平行光源は「太陽」だが、その特徴は一方向にしかフォトンが放出 されないことだ。太陽は地球から見れば点光源のようなものだが、あまりに 遠いので地球上ではフォトンの放射方向が(ほぼ)一方向になってしまう。 古典レイトレーシングでは大きさをもたずあらゆる場所で光が届いているか 判定するのだが、フォトンマッピングでは光源の範囲を制限してやらないと 無限にフォトンを放出しなければならなくなってしまう。 ということで今回はちょっとせこい手だが「面光源から一方向にのみフォトンが 放出される」ものを平行光源とすることにした。 イメージは「窓から入り込む太陽光」だ。

とすれば実装は平行光源のそれを参考に比較的簡単にできあがる。
data Light = (中略) SunLight { lcolor :: Color , lflux :: Flux , pos :: Position3 , nvec :: Direction3 , dir1 :: Direction3 , dir2 :: Direction3 , ldir :: Direction3 }
SunLightがそれ。以下、各関数の定義を示す。
generatePhoton (SunLight c _ p n d1 d2 d0) = do wl <- MT.randomIO :: IO Double t1 <- MT.randomIO :: IO Double t2 <- MT.randomIO :: IO Double let r = initRay (p + t1 *> d1 + t2 *> d2) d0 w = decideWavelength c wl return (w, r) getDirection (SunLight _ _ lp n d1 d2 dt) p | cos > 0.0 = [] | res == Nothing = [] | otherwise = [t *> dt'] where d = lp - p cos = n <.> d dt' = negate dt res = methodMoller 2.0 lp d1 d2 p dt' (u, v, t) = fromJust res getRadiance l@(SunLight (Color r g b) f _ _ _ _ _) (d:ds) = (Radiance (r * f) (g * f) (b * f)) : getRadiance l ds
generatePhotonは、面のどこからフォトンが放出されるかをランダムに
決めたらあとは指定した一方向へ放出している。
getDirectionはややこしそうだが、実のところ平行四辺形からその地点へ
光が放出されるかどうか、放出方向へ向かって交差判定しているのだ。
なおこの光源も「目に見える」が、窓という想定で空色にしておこう。
これで平行光源の定義もできた。画像を生成してみよう。また、フォトン数を 20万個から30万個に増やした時の画像も示す。まだら模様がいくぶん緩和されて いるのがわかる。影も滑らかで本物っぽい!

古典と比べるとその効果は歴然である。古典では間接光が表現できず ボールの形すら認識できない。一方フォトンマッピングでは間接光により 壁やボールがやんわりと照らされ形になっている!これこそフォトンマッピングの 醍醐味と言えるだろう。ただ、直接壁に当たる光については輪郭がぼやける。 これは点光源での影と同じである一定の範囲のフォトンを収集してしまうため 「直射日光」の当たる少し外側も引っ張られて非常に明るくなってしまうのだ。 フォトンマップ(下図)では輪郭がくっきりしているので、やはり収集方法の 問題だ。

とはいえ、平行光源については概ね満足できる結果といえよう。
3. まとめ
やっと拡散反射を実装できた。手間取ったが、拡散反射により得られる間接光には それだけの効果がある!とくに閉じた部屋へ太陽光(平行光源)が入射した時の表現は 思った以上に綺麗で(個人的には)感動ものだった。
次回は画質の向上をねたにしよう。
ここまでのソースはこちら。
DeepLearning(5): スペースリーク解消!
前回で形だけは写経が完成したわけだが、最後に書いたとおりひどいスペースリークが起こって使い物にならないことがわかった。今回はスペースリークの解消に取り組もう。(前回記事ではメモリリークと書いたが、Haskell界隈では(?)スペースリークと言うようだ。どう違うのか、同じなのかよくわからない)
(今回のソース)
1. 再帰の改善
いくつかのWebサイトを読んでみたが、Haskellは遅延評価のためにスペースリークを起こしやすいそうだ。素人には細かいことはわからないが、遅延評価のため必要になるまで計算を保留し、その情報をメモリ(ヒープ領域)に置くようだ。だから保留される計算が増えるほどメモリを消費するらしい。再帰といえばスタックオーバーフローだが、それは右再帰での話のようで、、、
さて計算が保留されるような処理がどこにあるのか、ということだがじつはさっぱりわからない。が、どうもfoldlのような左再帰で起こるらしいので、まずはメインループを疑ってみた。もとの実装は次のような感じ。
(Main-train.hs) main = do (中略) let is = [(epoch_ed st), (epoch_ed st - 1) .. (epoch_st st)] getTeachers = getImages (poolT st) (batch st) putF = putStatus tm0 (epoch_st st) (epoch_ed st) (opstep st) putStrLn "Training the model..." putF 0 (layers st) sampleE layers' <- trainLoop getTeachers sampleE putF (learnR st) (layers st) is (中略) trainLoop :: (Int -> IO [Trainer]) -> [Trainer] -> (Int -> [Layer] -> [Trainer] -> IO ()) -> Double -> [Layer] -> [Int] -> IO [Layer] trainLoop _ _ _ _ ls [] = return ls trainLoop getT se putF lr ls (i:is) = do ls' <- trainLoop getT se putF lr ls is teachers <- getT i let rls = tail $ map reverseLayer $ reverse ls' -- fist element isn't used dls = map (train ls' rls) teachers ls'' = update lr (transpose dls) ls' -- dls = diff of layers putF i ls'' se return ls''
このtrainLoopがメインループというかメイン再帰であるが、ご覧の通り珍妙なコードになっている。trainLoopは処理の最初でさらにtrainLoopを呼んでいる。これはこのループが学習によってレイヤをどんどん更新していくためで、書いた当時はその更新を表現する方法がこれしか思い浮かばなかったのだ。これが左再帰なのか深く考えていないが、わかりにくく汚いコードには違いないので書き直してみよう。foldlはアキュームレータという"変数"を使って計算結果で更新していくそうだが、これは使えそうだ。
trainLoopはIOがあるのでfoldlを使うことができないがfoldMが使えそうだ。一方で、Haskellのfoldlはスペースリークを起こしやすいとの記事もありfoldl'を使えとある。foldl'版のfoldMはないのかと思ったら下記のページに簡単な実装が書いてあった。
StackOverflow: Does Haskell have foldlM'?
これを使って書き直したのが下記のコード。
(Main-train.hs) main = do (中略) let is = [(epoch_st st) .. (epoch_ed st)] getTeachers = getImages (poolT st) (batch st) putF = putStatus tm0 (epoch_st st) (epoch_ed st) (opstep st) loopFunc = trainLoop' getTeachers sampleE putF (learnR st) putStrLn "Training the model..." putF 0 (layers st) sampleE layers' <- foldM' loopFunc (layers st) is (中略) foldM' :: (Monad m) => ([a] -> b -> m [a]) -> [a] -> [b] -> m [a] foldM' _ z [] = return z foldM' f z (x:xs) = do z' <- f z x z' `seq` foldM' f z' xs trainLoop' :: (Int -> IO [Trainer]) -> [Trainer] -> (Int -> [Layer] -> [Trainer] -> IO ()) -> Double -> [Layer] -> Int -> IO [Layer] trainLoop' getT se putF lr ls i = do teachers <- getT i let ls' = updateLayers lr teachers ls putF i ls' se return ls' updateLayers :: Double -> [Trainer] -> [Layer] -> [Layer] updateLayers lr ts ls = update lr ls (transpose dls) where rls = tail $ map reverseLayer $ reverse ls -- fist element isn't used dls = map (train ls rls) ts -- dls = diff of layers
ついでにtrainLoop'内も小ぎれいにしてコアとなる更新処理をupdateLayersに出しておいた。
trainLoop'は再帰がなくなり非常にすっきりした。また、ループのために追番リストを渡しているが、前は逆順だったのが正順に改まった。
で、大事なのはこれでスペースリークが改善するかだが、、、「ダメ」だった。やはりこの問題をきちんと理解せず表面的に再帰処理をどうこうしてもダメなんだろうなと思う。ただ、メインループの気色悪い実装が多少は改善したので、それでよしとしよう。
2. BangPattern
スペースリークの件でググるとBangPatternなるものに言及されている記事がいろいろ見つかる。先述の「計算が保留されてメモリに一時置かれたもの」(これをthunkというらしい)を"とっとと計算しつくす"ように指示するもののようだ(間違ってたらご指摘を)。
ということで、上記のメインループに使ってみた。BangPatternを使うにはソースファイルの先頭にその旨を書くようだ。
(Main-train.hs) : {-# LANGUAGE BangPatterns #-} (中略) foldM' :: (Monad m) => ([a] -> b -> m [a]) -> [a] -> [b] -> m [a] foldM' _ <font color="red">!z</font> [] = return z foldM' f <font color="red">!z</font> (x:xs) = do z' <- f z x z' `seq` foldM' f z' xs (中略) trainLoop' :: (Int -> IO [Trainer]) -> [Trainer] -> (Int -> [Layer] -> [Trainer] -> IO ()) -> Double -> [Layer] -> Int -> IO [Layer] trainLoop' getT se putF lr <font color="red">!ls</font> i = do : (中略) updateLayers :: Double -> [Trainer] -> [Layer] -> [Layer] updateLayers lr ts <font color="red">!ls</font> = update lr ls (transpose dls) :
foldM'、trainLoop'、updateLayersの引数についている"!“がその指定。とにかく手当たり次第入れてみた。が、「全滅」した。全く効果がない。。。
thunkをつぶすために deepseq を使うという記事もいくつかあったが、やってみようとすると対象のデータ型をNFData型クラスのインスタンスにする(?)とか、結局素人にはなすすべがなく断念した次第である。
3. hmatrixの採用
効果がありそうなことを試してもちゃんと原因を特定していないので無関係な場所に適用してしまっているのだろう。やっぱりもう少しちゃんと原因を探してみたい。
-1. 問題発生箇所はどこか
スペースリークに気づいたのは畳み込み層を含めた逆伝播処理(Aとしよう)が仕上がった時であり、その前の全結合層だけ逆伝播(Bとする)していた時は気にならなかった。なので両方の実行時のメモリ割り当てを比べてみた。
AもBも処理が進むたびにメモリをどんどん食っていくので、残念ながらスペースリークは前から起こっていたらしい。しかし、Aでは繰り返し1回で約30MB増えていくのに比べ、Bでは約1MBしか増えない。だからBでは500回程度の繰り返しではメモリが足りて問題に気づかなかったようだ。一方Aでは500回も繰り返すと15GB必要になる計算なのでとてもではないが私のPCでは無理だ。
Aの方が極端にメモリを食うので、Aで追加したコード(畳み込み・プーリングの逆伝播)を重点的に調べることにした。特に重そうな畳み込み層の逆伝播処理は次の通り。
(ConvLayer.hs) deconvolve :: Int -> [FilterC] -> Image -> Delta -> (Delta, Layer) deconvolve s fs im d = (delta, ConvLayer s (zip dw db)) where delta = convolve s fs $ addBorder s d db = map (sum . map sum) d -- delta B sim = slideImage s im dw = map (hadamard sim) d
delta =...はほぼ順伝播の処理そのままなので無視、その他を「ダミー(全部0のデータを代わりに与えたり空リストを渡したり)」に変更して実行してみた。
すると、使用メモリの増加が30MBから10MB程度になった!やはりここが悪いらしい。これら処理にはmapやsumなど再帰関数が多用されている。データは全て「リスト」で表現しており、処理内容からしてmapやsumを多用することは避けられない。どうしようもない?
-2. 思い切ってリストからhmatrixに書き換え
このプログラムでは型(ImageとかFilterCとか)は全てリストで定義してきた。これはまず標準の機能・ライブラリでやれるところまでやってみたかったから。リストでは処理が遅いのはわかっているのでゆくゆくはhmatrixとかRepaとかに移そうと思ってはいたが、速度改善のネタとしてとっておくつもりだったんだがなぁ。。。
だが私のレベルではリストを使いつつ問題を解決することができそうにない。とにかくリストをできるだけ使わないようにするしかないが、代わりに行列ライブラリを使うとして何を使うか。本命はRepaだった。高速化の一環でGPUを使った並列化も考えているため、Accelerateに書き方が似ているからだ(逆か)。
しかしこの記事ではRepaはどうもhmatrixに比べだいぶ遅いようだ。またRepaの解説記事も読んだが書き方が私にはとても難解で奇妙で理解しがたい。一方こちらのhmatrixの解説を読むと素直な書き方ができるようだし、ライブラリのページをみるといろいろ使えそうな関数が揃ってそうだ。ということで、hmatixに決定!
導入と設定は次の通り。
$ cabal install hmatrix
cabalファイルにも追加が必要だ。
(deeplearning.cabal) : executable train main-is: Main-train.hs -- other-modules: -- other-extensions: build-depends: base >=4.8 && <5.0 , mersenne-random >= 1.0 , containers , time , deepseq , hmatrix :
hmatrixは一次元配列相当のVectorと二次元のMatrixからなり三次元以上はなさそう。これらを使って既存の型を定義し直す。
(Image.hs,LayerType.hs) (before) type Plain = [[Double]] -- 2D: X x Y pixels type Class = [Double] -- teacher vector type ActFunc = [Double] -> [Double] type Kernel = [[Double]] type FilterF = [Double] (after) type Plain = Matrix R -- 2D: X x Y pixels type Class = Vector R -- teacher vector type ActFunc = Matrix R -> Matrix R type Kernel = Matrix R type FilterF = Matrix R
できるだけMatrixかVectorに変更した。RはDoubleと同じらしい。注意が必要なのがFilterFで、前の実装ではこれは[FilterF]とリストにしていた。今回これをFilterFに改めた。要は[[Double]]をMatrix Rに変えたのだ。
この変更により、既存の関数は引数の型合せが大変だったが、それよりも従来リストで書いていたものを全部新しい型を使って全面的に書き直すのに苦労した。特に畳み込み層、プーリング層。これらを見ていこう。
deep learning では行列を使うのが有効だと思うが、前回までのプログラムはあえてリストにしたため、例えば畳み込みで画像の一部を切り取るためにややこしくわかりにくい関数を作ってしまった。
今回型は行列なので、hmatrixの便利な関数subMatrixを使うことでそれが超簡単にできてしまった。逆に、これまで「一部を切り出して畳み込み、次を切り出して畳み込み」と直列処理?をしていたのを、切り取りを最初に一括で行い、それを順に畳み込むよう変更することになった。今回コードの畳み込み処理は次のよう。
(ConvLayer.hs: new) convolve :: Int -> [FilterC] -> Image -> Image convolve s fs im = map (convolveImage x iss) fs where pl = head im x = cols pl - (s - 1) y = rows pl - (s - 1) ps = [(i, j) | i <- [0..(x-1)], j <- [0..(y-1)]] iss = map subImage im subImage :: Plain -> Matrix R subImage i = fromColumns $ map (\p -> flatten $ subMatrix p (s, s) i) ps convolveImage :: Int -> [Matrix R] -> FilterC -> Plain convolveImage x iss (k, b) = reshape x $ cmap (+ b) $ vsum vs where vs = zipWith (<#) (toRows k) iss
面倒な行列の切り出しがsubMatrixで済んでしまうことは大きい。前のコードに比べかなり短くなった(28行から14行)。
(参考:前のコードの同じ部分)
(ConvLayer.hs: old) convolve :: Int -> [FilterC] -> Image -> Image convolve s fs im = map (convolveImage s im) fs convolveImage :: Int -> Image -> FilterC -> Plain convolveImage s im (ks, b) = sumPlains b (zipWith (convolvePlain s) ks im) sumPlains :: Double -> [Plain] -> Plain sumPlains b [] = repeat $ repeat b -- 2 Dimensions (X*Y) sumPlains b (p:ps) = zipWith f p (sumPlains b ps) where f :: [Double] -> [Double] -> [Double] f [] _ = [] f (a:[]) (b:_) = [a + b] f (a:as) (b:bs) = (a + b) : f as bs convolvePlain :: Int -> [Double] -> Plain -> Plain convolvePlain s k ps | len < s = [] | otherwise = convolveLine s k p : convolvePlain s k ps' where len = length ps p = take s ps ps' = tail ps convolveLine :: Int -> [Double] -> [[Double]] -> [Double] convolveLine s k ps | len < s = [] | otherwise = sum (zipWith (*) vs k) : convolveLine s k ps' where len = minimum $ map length ps vs = concatMap (take s) ps ps' = map tail ps
プーリング層も同様で、行列を小領域に区分けして処理していくため、subMatrixが活躍する。
こちらも始めに小領域を全部作って順に処理する形に変えたので、行数は31行から19行にへった。
(PoolLayer.hs: new) poolMax :: Int -> Image -> [Image] poolMax s im = [os, is] where pl = head im x = cols pl `div` s y = rows pl `div` s ps = [(i*s, j*s) | i <- [0..(x-1)], j <- [0..(y-1)]] (os, is) = unzip $ map (toPlain x y . maxPix s ps) im toPlain :: Int -> Int -> [Pix] -> (Plain, Plain) toPlain x y pls = ((x><y) op, (x><y) ip) where (op, ip) = unzip pls maxPix :: Int -> [(Int, Int)] -> Plain -> [Pix] maxPix s ps is = map (max' . toPix) ps where toPix :: (Int, Int) -> [Pix] toPix p = zip (concat $ toLists $ subMatrix p (s, s) is) [0.0..]
(参考:前の実装はこう)
(PoolLayer.hs: old) poolMax :: Int -> Image -> [Image] poolMax s im = [fst pixs, snd pixs] where pixs = unzip $ map unzipPix (poolMax' s im) unzipPix :: [[Pix]] -> ([[Double]], [[Double]]) unzipPix pixs = unzip $ map unzip pixs poolMax' :: Int -> Image -> [[[Pix]]] poolMax' s = map (poolMaxPlain s) poolMaxPlain :: Int -> Plain -> [[Pix]] poolMaxPlain s p = map (poolMaxLine s) ls where ls = splitPlain s p splitPlain :: Int -> Plain -> [[[Double]]] splitPlain s [] = [] splitPlain s p = p' : splitPlain s ps where (p', ps) = splitAt s p poolMaxLine :: Int -> [[Double]] -> [Pix] poolMaxLine _ [] = [] poolMaxLine s ls | len == 0 = [] | otherwise = pixs : poolMaxLine s ls' where len = length $ head ls pixs = max' $ zip (concatMap (take s) ls) [0.0 ..] ls' = map (drop s) ls
hmatrixの使用前後を比べてみるとわかるが、かなり作り方というか処理の流れが変わってしまった。関数は、ほとんど一から作りなおしたようなものだ。
ここで、テストコードに大いに助けられた。私はズボラなのでテストコードを書くのは嫌いで苦手だが、deep learningでは思った通りの変換ができているか確認しておかないと各層の実装間違いが後に響くため、いつもより多めにテストコードを入れていた。
前述の通り一部の関数はほぼ作り直しだったが、テストで得られる結果は前の実装と同じはずだ。データ型を変更したので入力・出力の形は異なるが結果の値は同じだ(見難いので一部改行を入れてある)。
(old code) >>> let filter = [ ([[1.0,2.0,3.0,4.0],[5.0,6.0,7.0,8.0]],0.25), ([[3.0,4.0,5.0,6.0],[7.0,8.0,1.0,2.0]],0.5), ([[5.0,6.0,7.0,8.0],[1.0,2.0,3.0,4.0]],0.75)] :: [FilterC] >>> let img1 = [ [[1.0,2.0,3.0],[4.0,5.0,6.0],[7.0,8.0,9.0]], [[4.0,5.0,6.0],[7.0,8.0,9.0],[1.0,2.0,3.0]]] :: Image >>> convolve 2 filter img1 [[[200.25,236.25], [173.25,209.25]], [[152.5,188.5], [233.5,269.5]], [[152.75,188.75], [197.75,233.75]]] (new code) >>> let filter = [ (fromLists [[1.0,2.0,3.0,4.0],[5.0,6.0,7.0,8.0]],0.25), (fromLists [[3.0,4.0,5.0,6.0],[7.0,8.0,1.0,2.0]],0.5), (fromLists [[5.0,6.0,7.0,8.0],[1.0,2.0,3.0,4.0]],0.75)] :: [FilterC] >>> let img1 = [ fromLists [[1.0,2.0,3.0],[4.0,5.0,6.0],[7.0,8.0,9.0]], fromLists [[4.0,5.0,6.0],[7.0,8.0,9.0],[1.0,2.0,3.0]]] :: Image >>> convolve 2 filter img1 [(2><2) [ 200.25, 236.25 , 173.25, 209.25 ],(2><2) [ 152.5, 188.5 , 233.5, 269.5 ],(2><2) [ 152.75, 188.75 , 197.75, 233.75 ]]
このように、テストで前と同じ結果であることを保証できないと内部実装をガラッと変えるのは怖い。今後テストコードをこまめに書くモチベーションアップにはなったと思う。
-3. 評価
(1) 学習結果(認識精度)
改善したプログラム(新CNNと呼ぼう)を例によって10回実行し、それぞれ認識精度と実行時間を計測した。前回は10回の平均を取ったが、これだと立ち上がりのタイミングが大きくぶれるため平均したら実際よりなだらかな微妙な曲線になってしまう。そこで今回は平均ではなく中間値でグラフを書いてみることにした。前回の、全結合層のみの値と畳み込み層までの値も同じく中間値でプロットしてみた。
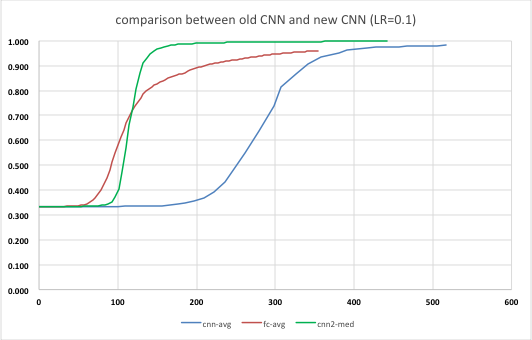
横軸が処理時間なので、新CNNの方が全結合層のみの場合より立ち上がるタイミングが遅いものの、学習効率が高く早期に95%を超えるのがわかる。今回の新CNNでは学習の進み方が圧倒的に速いためとても性能が高いと思う。
前回同様、処理にかかる時間を比較表にした。今回は500 epoch まで計測できたのでそれも追加した。
| 新CNN | CNN | 全結合層のみ学習 | |
|---|---|---|---|
| 処理時間(s) | 177 | 517 | 157 |
| 処理性能(epoch/s) | 1.130 | 0.387 | 1.273 |
| 認識精度(%) 200epochs | 97.8 | 97.5 | 74.2 |
| 認識精度(%) 500epochs | 99.6 | - | 95.1 |
単位時間あたりの処理量が、かなり全結合層のみ学習の時のそれに近づいた。一方で認識精度はさすが、かなり良い。
ということで、hmatrixを使った今回のバージョンでやっと本当の意味でのyusugomori実装の「写経」が完成したと言えるだろう。
(3) スペースリーク
そうそう、今回はスペースリークの解消が目的であった。新CNN実行時のメモリ使用量をtopコマンドで眺めていたが、繰り返し回数によらずだいたい60MBから70MBの間で推移し、多少増減するものの70MBを超えて増加することなく安定していた。スペースリークは解消したようだ!
-4. hmatrixを使った感想
このdeep learningのプログラムを実装するにあたり初めてhmatrixを知ったのだが、以下の点でこのライブラリをとてもよい。
わかり易い: 行列を作ったり、いろいろな操作をするのに込み入った記述はいらない。例えば 2x3行列を作りたければ
(2><2) [要素のリスト]と書けばよい。Numクラスのインスタンス(?): 足し算(+)、引き算(-)の関数はNumクラスのインスタンスでないと実装できないが hmatrixの
MatrixやVectorはそのインスタンスなので普通に足したり引いたりできる。以前別のプログラムでNumericPreludeを使って四則演算を自作したことがある。hmatrixはどうやっているのだろうか。今度ソースを眺めてみよう。便利関数多し: 高校や大学で習うような行列・ベクトルの演算はいわずもがな、CNNを作るのに「こんな関数が欲しいなぁ」と思うとちゃんと用意されている。
subMatrixはもちろん、要素を全部足すsumElementsや2つのベクトルの要素をそれぞれ掛けた値を行列にするouterなど、deep learningを実装するために作られたのではと思えるほど。なお、hmatrixを使った実装が終わり評価もほぼ終わったところでcorr2という関数を見つけた。これはどうやら「畳み込みをする関数」のようだ・・・。せっかく実装したのだが・・・。しかしcorr2を使うにはデータ型を変更しなくてはいけないみたいなので今回はパス。次の改善で考えよう。
4. おまけ
これまで何回か処理性能を評価してきたが、試行毎に学習の立ち上がりや認識精度の改善度合いに大きなばらつきがあることがわかった。試行毎の違いは全結合層および畳み込み層のフィルタの初期状態による。初期状態は乱数で設定するが、その値の範囲は次のように設定している。($x$をフィルタの設定値、$in$と$out$はその層の入力数・出力数とする)
(全結合層)
(畳み込み層)
一方でこの記事によると、deep learningの論文では学習効率を上げるためのフィルタの初期値として次の式が示されているという(私は原論文を読んでいないが)。
(活性化関数が$\tanh$のとき)
(活性化関数が$\mathrm{sigmoid}$のとき)
特に全結合層では大きく違いがある。これを論文で示された値にしたらどうなるか全結合層の実装で下記のように試してみた。
initFilterF :: Int -> Int -> IO FilterF
initFilterF k c = do
rs <- forM [1..k] $ \i -> do
w <- forM [1..c] $ \j -> do
r <- MT.randomIO :: IO Double
return ((r * 2.0 - 1.0) * a)
return (0.0:w)
return $ fromLists rs
where
a = 1.0 / fromIntegral c
↓
a = 4.0 * sqrt (6.0 / fromIntegral (c + k))
実行結果を表にしたものがこちら。
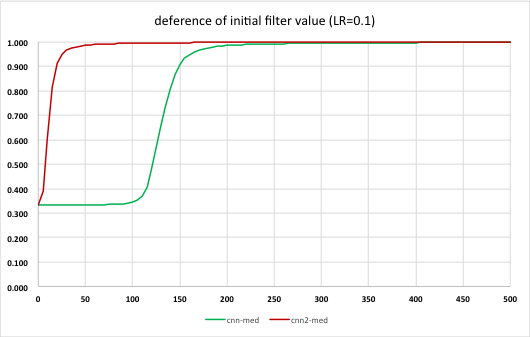
効果は歴然、学習効率が格段に向上していることがわかる。フィルタの初期値の違いがこれほど大きな差を生むとは驚きだ。逆に言えば、初期値を適切に与えないとなかなか学習が進まないということでもあり、おそらく個々の問題毎に最適な値が違うと思うので、これはもう試行錯誤しかないのだろう。ただ上記の論文ではその中でも比較的良い結果を得る指針かと。
5. まとめ
今回の改善で、やっとまともに動作するyusugomori実装の「写経」が完成し、初回に書いたステップ1が完了した。さすがに深層学習を一から勉強しないといけなかったのでしんどかった。。。
それでは次回、MNISTデータを使った学習(ステップ2)に取り組もう。
DeepLearning(4): CNNの逆伝播完成?
また時間が経ってしまった。畳み込み層の逆伝播のアルゴリズムを 理解するのに手間取ってしまった。。。気を取り直して、逆伝播の後半戦といこう。
1. 各層のおさらい
今回作っているプログラムは次のように11層のレイヤで画像を学習・評価している。
| No. | 層 | 実装 |
|---|---|---|
| 0 | 入力 | - |
| 1 | 畳み込み層1 | × |
| 2 | 活性化層1 | ○ |
| 3 | プーリング層1 | × |
| 4 | 畳み込み層2 | × |
| 5 | 活性化層2 | ○ |
| 6 | プーリング層2 | × |
| 7 | 平坦化層 | × |
| 8 | 全結合層1 | ○ |
| 9 | 活性化層3 | ○ |
| 10 | 全結合層2 | ○ |
| 11 | 活性化層4(出力) | ○ |
前回までで全結合層の逆伝播処理は説明したので、それらの処理は実装済み、 残るは×のついている層だ(平準化層、プーリング層、畳み込み層)。
その前に、前回のプログラムでは逆伝播において伝播させる誤差($\delta$)を
次のようにDoubleの一次元配列(というかリスト)とした。
type Delta = [Double]
しかしプーリング層や畳み込み層では、誤差は単純な一次元配列にならず、画像と 同じくXY平面がNチャネルという三次元のデータになる。ということで、次のように 改めた。すでに実装済みとした部分もこれに合わせて変更してある。
type Delta = Image -- (= [[[Double]]])
2. 各層の逆伝播処理
2-1. 平坦化(Flatten)層
前回は全結合層までの実装だったので、上記の表で言えば No.11 → No.8 までしか できていなかった。その次の平坦化層(No.7)はCNNの醍醐味である畳み込み層へ誤差を伝えるための 重要な転換点だ。が、実装は極めて単純だった。
unflatten :: Int -> Int -> Image -> Image unflatten x y [[ds]] = split y $ split x ds where split :: Int -> [a] -> [[a]] split _ [] = [] split n ds = d : split n ds' where (d, ds') = splitAt n ds
この層の逆伝播処理(unflatten)は、下層から一次元配列で伝わってきた誤差を
画像と同じ三次元配列に組み替えて上層に伝えること。
画像一枚の画素数(x,y)は引数で与える。
第三引数が微妙な形[[ds]]になっているのはDelta型を変更したから。
dsの型は[Double]だ。
ちなみに、入力されるデータ数がx,y画素できちんと割り切れることを想定して いて何のエラー処理もしていない。。。
2-2. プーリング層
プーリング層にはフィルタ情報がないので、下層から伝播してきた誤差($\delta$)を 更新して上層へ伝えれば良い。ただし、プーリング層の更新処理は特殊で、 他の層では誤差に何らかの計算処理をすればよいが、プーリング層では次のような ことをしないといけない。
- 順伝播の際に小領域(2x2とか3x3とか)から最大値を選択し、その画素の位置を 覚えておく。
- 逆伝播時は、誤差を順伝播で選択した画素の位置に分配し、小領域のそれ以外の画素には 0を設定する。
これを図にしたらこんな感じ。

前回のプログラムでは、プーリング層への入力画像は記録して いるものの、どの画素を選択したかという情報は記録していなかった。 yusugomori実装では、 選択画素を記録しておく代わりにプーリング層の「出力値=選択された画素」の値を使って、 小領域の値と順次比較することでどの画素を選択したかを特定するようになっている。 つまり誤差を求めるために「プーリング層の入力値と出力値の両方を使っている」 のだ。
しかし私の実装では、逆伝播を再帰で綺麗に(?)処理しようとしたために 誤差の計算は「各層の入力値のみ使う」形にしている。このシンプルな構造は 維持したい・・・。
結局「プーリング層の入力値を改竄する」ことにした(笑)。そのために 順伝播での処理をこう変えた。
- 画像を小領域に分割する(
poolMaxLine) - 小領域の各画素に番号を付ける(
zipで画素値と追番を組(Pix)にする) - 小領域中の画素の最大値を選択する(
max') - 選択した情報を集めると、(最大値,小領域中の追番)の組の集合になる
- 組の第一要素は下層へ伝える出力値、第二要素は「最大値画素の小領域内の
追番(の集合)」になる(
poolMax) - プーリング層は引数でもらった入力値をリストから削り、代わりに 「追番の集合」と出力値を返す
プログラムはこうなった。
type Pix = (Double, Double) : poolMax :: Int -> Image -> [Image] poolMax s im = [fst pixs, snd pixs] where pixs = unzip $ map unzipPix (poolMax' s im) : poolMaxLine :: Int -> [[Double]] -> [Pix] poolMaxLine _ [] = [] poolMaxLine s ls | len == 0 = [] | otherwise = pixs : poolMaxLine s ls' where len = length $ head ls pixs = max' $ zip (concatMap (take s) ls) [0.0 ..] ls' = map (drop s) ls max' :: [Pix] -> Pix max' [] = error "empty list!" max' [x] = x max' (x:xs) = maximum' x (max' xs) maximum' :: Pix -> Pix -> Pix maximum' a@(v1, i1) b@(v2, i2) = if v1 < v2 then b else a
Pixの組の定義で追番がDoubleなのは、追番の集合を
「画像」データとして保持するため型を合わせたから。poolMaxで
組のリストから「出力値」と「追番集合」を分離して返している。
poolMaxLine中の
pixs = max' $ zip (concatMap (take s) ls) [0.0 ..]
が各画素に追番を付けて最大値を選択しているところだ。
forwardLayer :: Layer -> Image -> [Image] forwardLayer (NopLayer) i = [i] forwardLayer (ActLayer f) i = [activate f i, i] forwardLayer (MaxPoolLayer s) i = poolMax s i forwardLayer (ConvLayer s fs) i = [convolve s fs i, i] :
forwardLayerにおいてプーリング層だけ他と異なっているのがわかるだろう。
他は全て引数のImage(=i)をその層で計算された出力値の後ろにくっつけて
返している。プーリング層では"i"をくっつけずPoolMaxの戻り値を使う。
これが「入力値を削る」という意味だ。
ここまでが順伝播での「準備段階」。逆伝播の処理は次の通り。
- 誤差と追番を組にする(
depoolMax内のconcatWith) - その組から小領域を生成する(追番のところは誤差値、それ以外は0)(
expand)
順伝播で頑張った分、逆伝播は単純になった。プログラムではこう。
depoolMax :: Int -> Image -> Delta -> (Delta, Layer) depoolMax s im d = (zipWith (concatWith (expand s 0.0)) im d, MaxPoolLayer s) where concatWith :: ([Int] -> [Double] -> [[Double]]) -> [[Double]] -> [[Double]] -> [[Double]] concatWith f i d = concat (zipWith f (map (map truncate) i) d) expand :: Int -> Double -> [Int] -> [Double] -> [[Double]] expand s r ps ds = map concat (transpose $ map split' $ zipWith ex ps ds) where split' = split s ex :: Int -> Double -> [Double] ex p d = take (s*s) (replicate p r ++ [d] ++ repeat r) split :: Int -> [a] -> [[a]] split s [] = [] split s xs | length xs < s = [xs] | otherwise = l : split s ls where (l, ls) = splitAt s xs
concatWithは少々ややこしいが追番集合を実数から整数に変換して誤差と
組にしたうえでexpandに渡している。
これで誤差を上層へ伝播できるわけだ。
2-3. 畳み込み層
(1) 誤差の計算
畳み込み層の逆伝播処理についてわかりやすく説明している書籍やWebサイトを 見つけられなかったので理解するのにかなり時間がかかってしまった。 唯一yusugomoriさんのblogが あったが、数式が苦手な私には理解は厳しく、結局yusugomori実装のソースを 追いかけることになった。。。
そしてやっと、逆伝播における畳み込み層の誤差計算の仕組みがわかった(つもり)。 順伝播と比較するとわかりやすいので図にしてみた。 (専門の方には初歩すぎるだろうが、本文章は自身の忘備録を兼ねて いるため軽く流していただきたい)

この例はフィルタ( $w$ )が2x2の場合である。まず順伝播では、入力画像の4つの画素から 出力の画素値を決めている。どの入力画素がどのフィルタ値と掛けられたか矢印を 色分けした。たとえば $x_{11}$ は $w$ の1番目(赤、 $w_1$ としよう)を掛けて $y_{11}$ の一部となっているので矢印は赤。 $y_{11}$ を式で書くと、
である。一方右の逆伝播の図では、今度は $y_{11}$ が下層から伝播された誤差である。 その誤差から上層へ伝える誤差の一つ $x_{11}$ への矢印はやはり赤であるから $w_1$ を掛けるのだ。つまり順伝播と逆をしているだけだ。
しかしプログラム上は $w$ の逆変換(?)である $w'$ (全結合層における $W$ の転置に相当)を 求めて使っている。これは「順伝播と同じ畳み込み処理をそのまま使って誤差を求める ことができる」からだ(と理解した)。
畳み込み層の順伝播処理では、出力画像の解像度は 入力画像のそれより小さくなる。例えばフィルタが2x2で入力が5x5ドットとすると 出力は(5-(2-1))x(5-(2-1))=4x4だ。逆伝播では下層から伝播した誤差データの 解像度(例えば4x4)が、求めたい誤差データの解像度(たとえば5x5)より小さいので そのままでは順伝播と同じ処理が使えない。そこで、誤差データに「外枠」を付けて 求めたい解像度より大きなサイズにする。右図では上と左に1ドットずつ"0"が並んでいる。 これがその「外枠」で、上下左右に同じ幅で追加する必要がある。幅はフィルタサイズ で決まる。2x2ならそれぞれ-1して1ドットずつ、3x3ならやはり-1して2ドットずつだ。
ここで、右図の左上の青点線で囲った中を見てみる。各画素から $x_{11}$ が 得られているが、 $y_{11}$ 以外は0なので $x_{11} = y_{11} \cdot w'_4 = y_{11} \cdot w_1$ だ。 左の順伝播での青点線の中のちょうど逆だ。一方、右図の赤点線の中は $x_{23}$ を 周りの $y$ からフィルタ $w'$ を掛けて求めている。これも順伝播での $x_{23}$ の 逆なだけ、ただ赤点線の中だけみるとフィルタが順伝播の逆順になっている。 これが $w$ の逆変換 $w'$ を使う理由。この $w'$ さえ用意してしまえば、あとは 順伝播の処理をそのまま呼び出せばよい。プログラムを見てみよう。
deconvolve :: Int -> [FilterC] -> Image -> Delta -> (Delta, Layer) deconvolve s fs im d = (delta, ConvLayer s (zip dw db)) where delta = convolve s fs $ addBorder s d :
この最後のdeltaが誤差を計算しているところ。fsには予め計算しておいた $w'$ が
入っている。下層からの誤差dにaddBorderで「外枠」を付けたら、
順伝播のconvolveを呼び出すだけ。ネタがわかってしまえば
プログラム自身はとても簡単であった。
(2) 勾配の計算
次に勾配( $\Delta W$ と $\Delta b$ )の計算について考える。 まず簡単な方から。 $\Delta b$ は、下層からの誤差を画像の各チャネルで 集計するだけ。各チャネルはX,Yの二次元データなのでそれを全て足せば良い。 式で書くとしたら下記のような感じか($c$はチャネル番号とする)。
$\Delta W$ の方はちょっとややこしい。下図を見て欲しい。

これは誤差、入力画像とも、とあるチャネルを取り出して $\Delta w$ (一つのフィルタということで小文字)を求める場合だ。それぞれ二次元データに なっている。要は $\delta$ と $a$ の該当する画素を掛け合わせて全て足すのだ。 ベクトルの内積のような感じ(行列も内積と言うのかな?)。 たとえば $\Delta w_1$ (赤)を求めるには、
を計算する。それ以外の要素もほぼ同じだが、 $a$ をフィルタの各要素の 場所ぶんだけずらした値を使う。各色の点線で囲った部分を使ってフィルタの 同じ色の要素を計算するわけだ。
これを誤差のチャネル数( $k$ とする)と入力画像のチャネル数( $c$ とする)を 掛けた $k \times c$ 枚計算すれば $\Delta W$ が出来上がる。
プログラムではこうなっている。
deconvolve :: Int -> [FilterC] -> Image -> Delta -> (Delta, Layer) deconvolve s fs im d = (delta, ConvLayer s (zip dw db)) where delta = convolve s fs $ addBorder s d db = map (sum . map sum) d -- delta B sim = slideImage s im dw = map (hadamard sim) d -- delta W slideImage :: Int -> Image -> [[Plain]] slideImage s im = map (concat . slidePlains s . slidePlain s) im (slide部分は省略) hadamard :: [[Plain]] -> Plain -> [[Double]] hadamard sim ds = map (map (mdot ds)) sim
まずslideImageで上記説明した各色の枠内の $a$ を取り出している。
ただし、右や下の使わない部分は、誤差dと突き合わせる際に無視されるため
わざわざ切り取っていない(例えば赤点線内は $a_{11}$ から $a_{14}$
までだがslideImageで得られるデータには $a_{15}$ も含まれている)。
そして、hadamardで誤差dとスライドした入力値を掛け合わせて
$\Delta W$ を求めている。
(3) フィルタ更新
(2)までで、ある教師データについて逆伝播の処理内容を説明した。 あとはバッチ1回で複数の教師データから得られた各 $\Delta W_i, \Delta b_i$ から フィルタの更新をすればよい。これは全結合の時と同じ式で計算できる。
この部分はプログラムではこうしている。
updateConvFilter :: Int -> [FilterC] -> Double -> [Layer] -> Layer updateConvFilter s fs lr dl = ConvLayer s $ zip ks' bs' where sc = lr / fromIntegral (length dl) (ks , bs ) = unzip fs (kss, bss) = unzip $ map unzip $ strip dl dbs = vscale sc $ vsum bss dks = map (mscale sc . msum) $ transpose kss bs' = vsub bs dbs ks' = zipWith msub ks dks strip :: [Layer] -> [[FilterC]] strip [] = [] strip (ConvLayer s fs:ds) = fs:strip ds strip (_:ds) = strip ds -- if not ConvLayer
引数fsが更新前のフィルタ($W$や$b$)、dlに各教師データから
学習で得られた $\Delta W$ と $\Delta b$ が入っている。これを上式に
当てはめて計算するのだ。
さあ、プログラムは完成した!
3. 評価
それでは早速出来上がったプログラムを実行して学習をさせてみよう。 (ソースはここ)
$ cabal clean $ cabal build : $ ./dist/build/train/train Initializing... Training the model... iter = 0/200 accuracy = 0.3333333333 time = 0.13968s iter = 5/200 accuracy = 0.3333526481 time = 11.021087s iter = 10/200 accuracy = 0.3333741834 time = 21.513648s iter = 15/200 accuracy = 0.3334006436 time = 33.707092s iter = 20/200 accuracy = 0.3334352183 time = 45.034608s iter = 25/200 accuracy = 0.3334818706 time = 55.7984s :
3-1. 前回分(全結合層のみ)との比較
(1) 学習結果(認識精度)
上記のプログラムを10回実行し、それぞれ認識精度と実行時間を計測した。 今回epoch数は200(前回は500)としたが理由は後述する。結果は次のグラフの とおり。

点線が各試行時の実測値、太いオレンジの実線が10回の平均だ。各試行では 認識精度が向上する時期(epoch)に大変ばらつきがある。これは全結合層の 学習でも同じだったが、最初にランダムに設定するフィルタ初期値が良くない からだと思われる。このように向上する時期がバラバラなので、 平均を取るとなんだか緩やかに学習が進むように見えてしまう。。。
次にyusugomori実装と比較してみる。上記の平均がオレンジ、yusugomori実装は 赤だ。参考までに前回の全結合のみの場合の平均(青)も比較のため入れた。

オレンジは上述の通り平均値のためなんだかふらついて変だが、最終的には ほぼ同程度の認識精度が得られている。前のグラフを見れば、認識精度の 向上具合はyusugomori実装と比べても遜色ないと思われる。 (実は逆伝播処理の「値の正しさ」はきちんと検証していないのだが、 この結果をみるとそんなに外していないのかな?ということでよしとする)
(2) 処理時間
ただ、いいことばかりではない。 畳み込み層まで逆伝播させたため、学習にかかる時間は逆に増えてしまった。 200 epoch実行時の結果を次表に示す。
| CNN | 全結合層のみ学習 | |
|---|---|---|
| 処理時間(s) | 517 | 157 |
| 処理性能(epoch/s) | 0.387 | 1.273 |
| 認識精度(%) 200epochs | 97.5 | 74.2 |
| 認識精度(%) 500epochs | - | 95.1 |
このように、同じ時間で処理できるepoch数が1/3以下に落ちてしまった。 さすがに複雑な畳み込み層/プーリング層の逆伝播処理は負荷が高い・・・。 同じepoch数ではさすがにCNNの方が認識精度が格段に高い。しかし全結合層のみの 学習でも500 epochs続ければ95%を超えるわけで、結局時間と得られる精度は どうなるかと思ってプロットしてみたのが次のグラフ。

このように、処理時間と認識精度を秤にかけると、畳み込み層まで逆伝播させたときは、 得られる精度に対しあまりアドバンテージがないように思える。もちろん、 認識精度を99%以上まで非常に高くするためには畳み込み層の学習が 必要なのだろうと思うが。
一方で、当然ながら私の実装のまずさもあるだろう。やたら再帰を使うとか 自分でも頭が混乱するような処理になっているので、もっと簡潔な実装に 改められたら改善するかもしれない。今後の課題の一つだ。
3-2. メモリリーク!?
さて、表題に「逆伝播完成?」とクエスチョンを付けた理由がこれだ。 epoch数を200に下げた理由も。
やっとできたと思ってepoch数500で実行してみるとなかなか終わらない。
開始時は1 epochの処理に約2秒かかったので単純計算では1000秒になるが
30分経っても350程度。おかしいと思ってtopコマンドでプロセスを見て
みたらメモリを10GBも食っていたのですぐ停止した!
気を取り直してもう一度実行したときのtopコマンドの出力がこれ。train
プロセスが大量のメモリを消費しているのがわかる。これは繰り返し回数が
だいたい180ぐらいのときの状態。
Processes: 162 total, 3 running, 159 sleeping, 639 threads 00:22:32 Load Avg: 1.99, 1.98, 1.80 CPU usage: 8.48% user, 32.11% sys, 59.40% idle SharedLibs: 92M resident, 33M data, 6516K linkedit. MemRegions: 23895 total, 477M resident, 29M private, 103M shared. PhysMem: 4080M used (1131M wired), 14M unused. VM: 471G vsize, 623M framework vsize, 71855224(48041) swapins, 73935000(0) swapo Networks: packets: 631497/460M in, 456172/62M out. Disks: 2706786/300G read, 1541857/302G written. PID COMMAND %CPU TIME #TH #WQ #PORT MEM PURG CMPRS PGRP 25694 train 81.4 08:49.94 1/1 0 10 1064M- 0B 4044M+ 25694 0 kernel_task 76.5 02:28:47 114/7 0 2 443M- 0B 0B 0 :
Macのメモリ管理についてはよく知らないが、trainプロセスの使用メモリが
1064M、CMPRSが4044Mで、合わせて5100M=5GBほども消費している。
これはいただけない。
本実装ではやたら(無駄に?)再帰を使ってしまっているが、その効率が
悪いのかもと思いつつ、消費メモリが増える一方なのはヒープ領域を
やたら使っているのだろう。ググると、foldl'を使えとかサンクがどうとか
いろいろあるみたいだが、簡単には解決しそうになかったので今回はここまで。
対策は次回に頑張ろうと思う。
4. まとめ
今回でやっと一通りCNNが 実装 できた。学習能力も手本としたyusugomori実装と同等のものができた。 しかしながら、上述のとおりメモリを大量に消費するという問題を抱えたままで、 このままでは全く実用に耐えない。
次回はこの問題を解決させたいと思う(できないかも・・・)。